Empirical Methods in Finance

Practicing 6

Henrique C. Martins

Panel Data

Panel Data

library(ggplot2)
library(ggthemes)
library(readxl) 
library(jtools) # for nice tables of models - https://cran.r-project.org/web/packages/jtools/vignettes/summ.html#summ
data <- read_excel("files/data.xls")

After uploading the data, tell R the data is panel. You need two identifiers: one for the cross-sectional part (usually, firms in accounting & finance research), and other for the time-series part (usually, year but sometimes can be quarter). The following example uses a panel wit quarterly data.

I am also creating an identifier for industries, which might be useful.

library(dplyr)
data <- data %>% group_by(id )                %>% dplyr::mutate(id_firm = cur_group_id())
data <- data %>% group_by(setor_economatica)  %>% dplyr::mutate(id_ind = cur_group_id())

Now, I am stating to r that I have a dataset in a panel structure.

library(plm)
data <- pdata.frame(data, index=c("id_firm","year"))

OLS, Panel, Fixed effects, and Random Effects

Let’s attach the dataset to make things easier.

attach(data)

Let’s inspect the dataset. First, let’s see how many observations we have by country:

library('plyr')
count(country)
   x freq
1 AR 1497
2 BR 6804
3 CL 3050
4 CO  483
5 MX 2315
6 PE 1928

Now, by year.

count(year)
      x freq
1  1995  624
2  1996  676
3  1997  743
4  1998  749
5  1999  738
6  2000  739
7  2001  681
8  2002  671
9  2003  666
10 2004  687
11 2005  679
12 2006  685
13 2007  739
14 2008  722
15 2009  727
16 2010  717
17 2011  719
18 2012  706
19 2013  701
20 2014  690
21 2015  669
22 2016  663
23 2017  686

OLS, Panel, Fixed effects, and Random Effects

Now, by industry.

count(setor_economatica)
                   x freq
1       Agro e Pesca  832
2    Alimentos e Beb 1537
3           Comércio 1117
4         Construção  806
5  Eletroeletrônicos  332
6   Energia Elétrica 1539
7    Máquinas Indust  259
8          Mineração  693
9   Minerais não Met  587
10            Outros 2860
11  Papel e Celulose  299
12    Petróleo e Gas  522
13           Química  859
14 Siderur & Metalur 1104
15  Software e Dados   75
16  Telecomunicações  770
17            Textil  845
18 Transporte Serviç  517
19  Veiculos e peças  524

Generating variables

Let’s generate some variables to use later.

data$lev1 <- Debt / (Debt + Equity.market.value)
data$lev2 <- Debt / Total.Assets
data$wc_ta <- wc  / Total.Assets 
data$cash_ta <- cash / Total.Assets
data$div_ta <- Dividends / Total.Assets
data$fcf_ta <- Free.cash.flow / Total.Assets
data$tang_ta <- tangible / Total.Assets
data$roa2 <- roa / 100
library(SciViews)
data$size1  <- ln(Total.Assets)

Generating variables

Notice that most variables are ratios and thus are expected to fall in the 0-100% range.

There is one important exception: Size. Size in this example is the natural logarithm of Total Assets (sometimes, studies use the natural logarithm of Total Sales). Taking the natural logarithm is a traditional decision in this type of research.

So, why did I do that in Size but not in the others?

Generating variables

In many cases, you want to use relative differences or percentages change. For instance, GDP growth is usually measured as the growth of each year over the previous year. The same is true for stock prices.

\[GDP\; growth = \frac{GDP_t - GDP_{t-1}}{GDP`{t-1}}\]

This is possible because you always have a previous value to use as base for comparison.

Generating variables

In many cases, you do not have such base for comparison. This is the case of a firm’s Total Assets. What is the natural base for Total Assets? No answer.

Therefore, you take the natural logarithm so that you minimize this concern.

Additionally, keep in mind that the empirical values of Total Assets are often very dissimilar and with huge magnitude. Consider two firms, one with 1 million of total assets, the other with 1 billion. Assume that both firms increased throughout one year their total assets by 1 million. The first firm is twice the size of before, but 1 million make little difference for a billion dollar firm. Taking the logarithm helps you to have a similar base and mitigate the magnitude effect of these changes.

Summary statistics

library(vtable)
sumtable(data, vars = c('lev1' , 'lev2' , 'wc_ta', 'cash_ta',  'size1'  , 'fcf_ta' , 'div_ta', 'roa' , 'tang_ta'))
Summary Statistics
Variable N Mean Std. Dev. Min Pctl. 25 Pctl. 75 Max
lev1 12708 0.35 0.28 0 0.11 0.55 1
lev2 12706 0.41 3.7 0 0.095 0.37 244
wc_ta 15584 -0.025 2.5 -139 -0.015 0.22 1
cash_ta 15056 0.073 0.1 0 0.01 0.096 1
size1 15686 20 2 7.3 18 21 27
fcf_ta 12426 0.091 7.4 -35 0.019 0.066 818
div_ta 10295 0.023 1.4 -0.073 0 0.0043 136
roa 13689 1.6 378 -3656 -0.47 2.4 43650
tang_ta 15600 0.4 0.25 0 0.19 0.59 1.1

Winsorization

Some of the variables have weird values. For instance, the variable \(\frac{Free cash flow}{Total Assets}\) has a maximum value of 817. It means that there is one firm-year observation in which the cash flow of that firm in that year is 817 times the firm’s total assets. This is very odd to say the least.

To avoid this type of problem, we can winsorize our variables.

library(DescTools)
data$w_lev1     <- Winsorize(data$lev1   , probs = c(0.01, 0.99) , na.rm = TRUE) 
data$w_lev2     <- Winsorize(data$lev2   , probs = c(0.01, 0.99) , na.rm = TRUE) 
data$w_wc_ta    <- Winsorize(data$wc_ta  , probs = c(0.01, 0.99) , na.rm = TRUE) 
data$w_cash_ta  <- Winsorize(data$cash_ta, probs = c(0.01, 0.99) , na.rm = TRUE) 
data$w_size1    <- Winsorize(data$size1  , probs = c(0.01, 0.99) , na.rm = TRUE) 
data$w_fcf_ta   <- Winsorize(data$fcf_ta , probs = c(0.01, 0.99) , na.rm = TRUE) 
data$w_div_ta   <- Winsorize(data$div_ta , probs = c(0.01, 0.99) , na.rm = TRUE) 
data$w_roa      <- Winsorize(data$roa    , probs = c(0.01, 0.99) , na.rm = TRUE) 
data$w_tang_ta  <- Winsorize(data$tang_ta, probs = c(0.01, 0.99) , na.rm = TRUE)

Panel data

Multiple times are always helpful. That is, in a panel dataset, you have many observations of the same unit in different time periods. This is helpful because you observe the evolution of that unit. Also, this allows to control for time-invariant unobserved heterogeneity at the unit level.

A general representation of a regression using panel data is:

\[Y_{t,i} = \alpha + \beta \times X_{t,i} + \epsilon_{t,i}\]

Notice that each variable has two subscripts, t represents the year = t, and i represents the unit = i. This type of notation is common in empirical research.

Functional form of relationships

As mentioned before, in many cases, you want to use the logarithm of a variable. This changes the interpretation of the coefficients you estimate.

We have three possible scenarios for regression’s functional forms.

  • log-log regression: both Y and X are in log values \(ln(Y) = \alpha + \beta \times ln(X) + \epsilon\). The interpretation of \(\beta\) in this case is: \(y\) is \(\beta\) percent higher on average for observations with one percent higher \(x\).

  • log-level regression: both Y and X are in log values \(ln(Y) = \alpha + \beta \times X + \epsilon\). The interpretation of \(\beta\) in this case is: \(y\) is \(\beta\) percent higher on average for observations with one unit higher \(x\).

  • level-log regression: both Y and X are in log values \(Y = \alpha + \beta \times ln(X) + \epsilon\). The interpretation of \(\beta\) in this case is: \(y\) is \(\frac{\beta}{100}\) units higher on average for observations with one percent higher \(x\).

Important note: the misspecification of x’s is similar to the omitted variable bias (OVB).

OLS

This is a plain OLS model using the original data (i.e., not winsorized yet).

ols <- lm(lev1 ~ size1 + fcf_ta + roa + tang_ta + cash_ta + div_ta, data = data)
summary(ols)

Call:
lm(formula = lev1 ~ size1 + fcf_ta + roa + tang_ta + cash_ta + 
    div_ta, data = data)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.44535 -0.19888 -0.04651  0.16032  1.40432 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -0.024252   0.031814  -0.762 0.445911    
size1        0.018368   0.001564  11.741  < 2e-16 ***
fcf_ta       0.160553   0.105327   1.524 0.127473    
roa         -0.001686   0.001054  -1.600 0.109642    
tang_ta      0.049239   0.012935   3.807 0.000142 ***
cash_ta     -0.476372   0.031985 -14.893  < 2e-16 ***
div_ta      -1.112794   0.106868 -10.413  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.2462 on 6878 degrees of freedom
  (9192 observations deleted due to missingness)
Multiple R-squared:  0.07463,   Adjusted R-squared:  0.07382 
F-statistic: 92.45 on 6 and 6878 DF,  p-value: < 2.2e-16

OLS

A nicer looking table.

library(jtools)
export_summs(ols, digits = 3 , model.names = c("OLS") )
OLS
(Intercept) -0.024    
(0.032)   
size1 0.018 ***
(0.002)   
fcf_ta 0.161    
(0.105)   
roa -0.002    
(0.001)   
tang_ta 0.049 ***
(0.013)   
cash_ta -0.476 ***
(0.032)   
div_ta -1.113 ***
(0.107)   
N 6885        
R2 0.075    
*** p < 0.001; ** p < 0.01; * p < 0.05.

OLS

Now, we are using the winsorized data.

w_ols <- lm(w_lev1 ~ w_size1 + w_fcf_ta + w_roa + w_tang_ta + w_cash_ta + w_div_ta, data = data)
#summary(w_ols)
export_summs(ols,w_ols ,model.names = c("OLS","OLS (winsorized)"))
OLS OLS (winsorized)
(Intercept) -0.02     -0.17 ***
(0.03)    (0.03)   
size1 0.02 ***        
(0.00)           
fcf_ta 0.16            
(0.11)           
roa -0.00            
(0.00)           
tang_ta 0.05 ***        
(0.01)           
cash_ta -0.48 ***        
(0.03)           
div_ta -1.11 ***        
(0.11)           
w_size1         0.03 ***
        (0.00)   
w_fcf_ta         -0.03    
        (0.11)   
w_roa         -0.01 ***
        (0.00)   
w_tang_ta         0.06 ***
        (0.01)   
w_cash_ta         -0.50 ***
        (0.03)   
w_div_ta         -3.03 ***
        (0.19)   
N 6885        6885       
R2 0.07     0.15    
*** p < 0.001; ** p < 0.01; * p < 0.05.

Heterogeneity across countries

There is a huge literature on capital structure decisions. Let’s see the heterogeneity of leverage across countries. Thus, it makes sense to control for this type of heterogeneity somehow.

library(gplots)
plotmeans(lev1 ~ country, data = data)

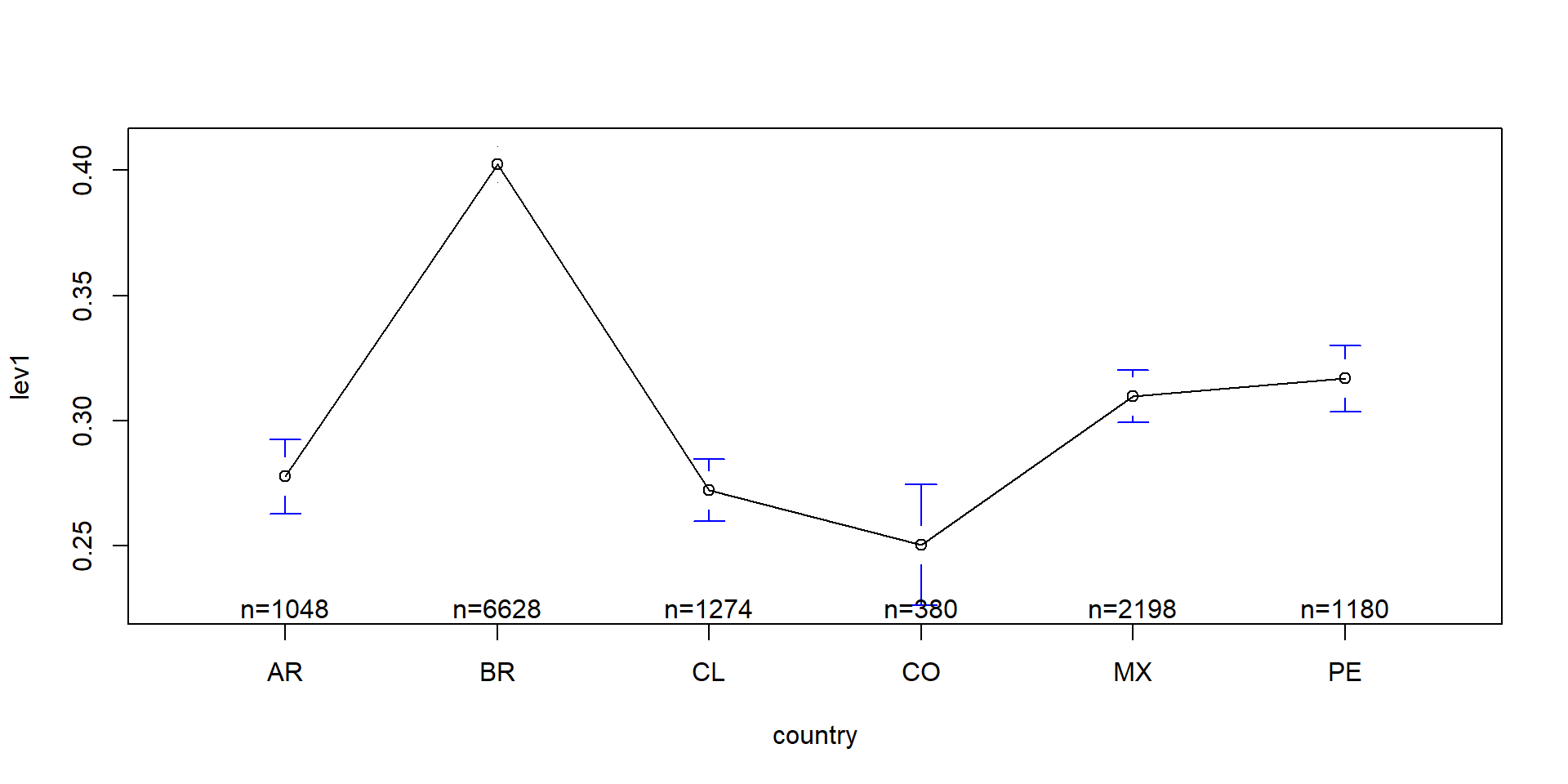
FE Country

The following example uses fixed effects for countries. Notice that one country is missing.

fe_c <- lm(lev1 ~ size1 + fcf_ta + roa + tang_ta + cash_ta + div_ta  + factor(country) , data = data)
export_summs(fe_c)
Model 1
(Intercept) -0.02    
(0.03)   
size1 0.01 ***
(0.00)   
fcf_ta 0.11    
(0.10)   
roa -0.00    
(0.00)   
tang_ta 0.09 ***
(0.01)   
cash_ta -0.48 ***
(0.03)   
div_ta -1.14 ***
(0.11)   
factor(country)BR 0.10 ***
(0.01)   
factor(country)CL 0.02    
(0.01)   
factor(country)CO 0.11 ***
(0.03)   
factor(country)MX 0.03 ** 
(0.01)   
factor(country)PE 0.09 ***
(0.01)   
N 6885       
R2 0.10    
*** p < 0.001; ** p < 0.01; * p < 0.05.

FE Country

Now, we are using fixed effects for countries and years.

fe_cy <- lm(lev1 ~ size1 + fcf_ta + roa + tang_ta + cash_ta + div_ta  + factor(country) + factor(year), data = data)
export_summs(fe_c, fe_cy)
Model 1 Model 2
(Intercept) -0.02     -0.01    
(0.03)    (0.04)   
size1 0.01 *** 0.02 ***
(0.00)    (0.00)   
fcf_ta 0.11     0.08    
(0.10)    (0.10)   
roa -0.00     -0.00    
(0.00)    (0.00)   
tang_ta 0.09 *** 0.09 ***
(0.01)    (0.01)   
cash_ta -0.48 *** -0.44 ***
(0.03)    (0.03)   
div_ta -1.14 *** -1.12 ***
(0.11)    (0.10)   
factor(country)BR 0.10 *** 0.10 ***
(0.01)    (0.01)   
factor(country)CL 0.02     0.01    
(0.01)    (0.01)   
factor(country)CO 0.11 *** 0.08 *  
(0.03)    (0.03)   
factor(country)MX 0.03 **  0.01    
(0.01)    (0.01)   
factor(country)PE 0.09 *** 0.05 ** 
(0.01)    (0.02)   
factor(year)1996         -0.03    
        (0.03)   
factor(year)1997         -0.08 *  
        (0.03)   
factor(year)1998         0.02    
        (0.03)   
factor(year)1999         -0.03    
        (0.03)   
factor(year)2000         0.03    
        (0.03)   
factor(year)2001         0.04    
        (0.03)   
factor(year)2002         0.04    
        (0.03)   
factor(year)2003         -0.01    
        (0.03)   
factor(year)2004         -0.06    
        (0.03)   
factor(year)2005         -0.08 *  
        (0.03)   
factor(year)2006         -0.10 ***
        (0.03)   
factor(year)2007         -0.12 ***
        (0.03)   
factor(year)2008         -0.03    
        (0.03)   
factor(year)2009         -0.12 ***
        (0.03)   
factor(year)2010         -0.13 ***
        (0.03)   
factor(year)2011         -0.08 ** 
        (0.03)   
factor(year)2012         -0.07 ** 
        (0.03)   
factor(year)2013         -0.06 *  
        (0.03)   
factor(year)2014         -0.05    
        (0.03)   
factor(year)2015         0.00    
        (0.03)   
factor(year)2016         -0.04    
        (0.03)   
factor(year)2017         -0.07 ** 
        (0.03)   
N 6885        6885       
R2 0.10     0.13    
*** p < 0.001; ** p < 0.01; * p < 0.05.

FE Firms

The most usual regression we estimate in Accounting & Finance is a panel using firms as units. Imagine that you are including one dummy for each firm, just as we included a dummy for each country in the previous example. This is the way to do it.

The strength of a firm fixed effect model is that it controls for time-invariant unobserved heterogeneity at the firm level.

That is, if there is an omitted variable in your model (something that is constant over time that you cannot measure because you do not observe, for instance, the quality of the managerial team), you should use firm fixed effects.

FE is a very traditional and accepted solution in this type of research because our models are always a representation of reality, we can never be sure we are controlling for everything that is important. By including a firm FE you are, at least, safe that you are controlling of omitted variables that do not change over time at the firm level. That is, Firm FE mitigates concerns of omitted variable bias of time-invariant at the firm level.

On top of the firm FE, it is always a good idea to include year FE at the same time, as follows. You do not need to present them in your final paper, but you need to mention them.

fe <- plm(w_lev1 ~ w_size1 + w_fcf_ta + w_roa + w_tang_ta + w_cash_ta + w_div_ta + factor(year) , data = data, model="within")
export_summs(fe, coefs = c("w_size1","w_div_ta","w_fcf_ta","w_roa","w_tang_ta","w_cash_ta"),  digits = 3 , model.names = c("FE") )
FE
w_size1 0.076 ***
(0.004)   
w_div_ta -0.894 ***
(0.152)   
w_fcf_ta 0.453 ***
(0.117)   
w_roa -0.009 ***
(0.001)   
w_tang_ta 0.176 ***
(0.019)   
w_cash_ta -0.304 ***
(0.029)   
nobs 6885        
r.squared 0.215    
adj.r.squared 0.086    
statistic 57.872    
p.value 0.000    
deviance 108.418    
df.residual 5914.000    
nobs.1 6885.000    
*** p < 0.001; ** p < 0.01; * p < 0.05.

More technically (but really not that much), a firm FE model can be represented as follows. That is, you include one fixed term for each firm (again, except for the first firm). Also, I am adding the year FE in the equation below.

\[Y_{t,i} = \beta \times X_{t-1,i} + \alpha_i + \alpha_t+ \epsilon_{t,i}\]

Technically, the inclusion of the FE acts as a transformation of Y and X into differences such as \(y_{t,i} - \bar{y_i}\) and \(x_{t,i} - \bar{x_i}\), where \(\bar{y_i}\) is the mean value of y across all time periods for unit i. As a result, in FE regressions, \(\beta\) shows how much larger y is compared to its mean within the cross-sectional unit. That is, compare two observations of x that are different in terms of their value x compared to the i-specific mean. On average, x is larger that average x by \(\beta\).

Thus, a FE model is a within-unit comparison model and the model is not affected by whether the unit has larger average of X or Y. That is, the estimates are not affected by unobserved confounders that affect either x or y in the same way in all time periods.

Important question: Can you include firm FE and country FE at the same time in a regression? The answer is no. If you try, all the country FE will be dropped due to colinearity with firm FE.

Final notes on FE models:

  1. Notice there is no intercept in the table above. The reason is that the model includes \(i\) intercepts, one for each firm. In some cases, some softwares report an intercept value that is the average of all intercepts. But that is of little value to us.

  2. There are two possible r-squares in FE models: within R-squared and the R-squared (the traditional one). The first is more adequate, because the second uses all intercepts as explanatory variables of y and thus overstates the magnitude of the model’s explanatory power.

OLS vs FE

At the end of the day, you never can be sure that the FE model is better. So, we can test if it is an improvement over OLS, as follows.

If the p-value low enough then the fixed effects model is the path to go.

pFtest(fe, ols)

    F test for individual effects

data:  w_lev1 ~ w_size1 + w_fcf_ta + w_roa + w_tang_ta + w_cash_ta +  ...
F = 17.45, df1 = 964, df2 = 5914, p-value < 2.2e-16
alternative hypothesis: significant effects

Random Effects

An alternative to FE models is the RE (random effects) models. In FE models, we assume \(\alpha_i\) is correlated with the other X variables. This makes sense since the unobserved time-invariant characteristics of a firm is expected to be correlated with the observed characteristics of that firm.

If we believe that \(\alpha_i\) is not correlated with X, we should use a RE model. You can estimate as follows.

re <- plm(w_lev1 ~ w_size1 + w_fcf_ta + w_roa + w_tang_ta + w_cash_ta + w_div_ta  , data = data, model="random") 
export_summs(fe, re, coefs = c("w_size1","w_div_ta","w_fcf_ta","w_roa","w_tang_ta","w_cash_ta"),  digits = 3 , model.names = c("FE", "RE") )
FE RE
w_size1 0.076 *** 0.033 ***
(0.004)    (0.003)   
w_div_ta -0.894 *** -1.336 ***
(0.152)    (0.157)   
w_fcf_ta 0.453 *** 0.307 ** 
(0.117)    (0.112)   
w_roa -0.009 *** -0.009 ***
(0.001)    (0.001)   
w_tang_ta 0.176 *** 0.149 ***
(0.019)    (0.016)   
w_cash_ta -0.304 *** -0.410 ***
(0.029)    (0.029)   
nobs 6885         6885        
r.squared 0.215     0.144    
adj.r.squared 0.086     0.144    
statistic 57.872     856.420    
p.value 0.000     0.000    
deviance 108.418     146.431    
df.residual 5914.000     6878.000    
nobs.1 6885.000     6885.000    
*** p < 0.001; ** p < 0.01; * p < 0.05.

RE vs FE

If you want to test which model is best suited to your dataset, you can test as follows. If the p-value is significant then use FE, if not use RE.

phtest(fe, re)

    Hausman Test

data:  w_lev1 ~ w_size1 + w_fcf_ta + w_roa + w_tang_ta + w_cash_ta +  ...
chisq = 9718.9, df = 6, p-value < 2.2e-16
alternative hypothesis: one model is inconsistent

THANK YOU!

QUESTIONS?

Henrique C. Martins

[Henrique C. Martins] [henrique.martins@fgv.br][Do not use without permission]