Empirical Methods in Finance

Practicing 4

Henrique C. Martins

Selection problem

pop <- 5000
sample <- 50
set.seed(1235)
x <- runif(pop, min=0, max=5000)
y <- x/5 + runif(pop, min=0, max=5000)
df <- data.frame(x,y)

Imagine that the population contains 5000 units, from which you can observe only 50.

You want to run a linear model to understand the relationship between x and Y.

The “true” beta of this relationship is as follows. By “true” I mean the beta you would get should you observe the population (remember though that you don’t).

summary(lm(df$y ~ df$x))


Call:
lm(formula = df$y ~ df$x)

Residuals:
     Min       1Q   Median       3Q      Max 
-2527.44 -1230.21     4.28  1246.20  2510.94 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 2.549e+03  4.103e+01   62.13   <2e-16 ***
df$x        1.871e-01  1.407e-02   13.30   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1435 on 4998 degrees of freedom
Multiple R-squared:  0.03416,   Adjusted R-squared:  0.03397 
F-statistic: 176.8 on 1 and 4998 DF,  p-value: < 2.2e-16

So the “true” beta is 0.187. And the t-stat is 13.296

Plotting this relationship in a graph, you get:

library(ggplot2)
library(ggthemes)
ggplot(df) +  geom_point( aes(x=x, y=y), color = "lightblue") +
              geom_smooth(data = df, aes(x=x, y=y) , method = lm) + 
              theme_solarized() + 
              labs(title = paste("Beta is" , round(summary(lm(df$y ~ df$x))$coefficients[2,1], 3) , 
                                 ", Beta t-stat is" , round(summary(lm(df$y ~ df$x))$coefficients[2,3], 3) , 
                                 ", R2 is" , round(summary(lm(df$y ~ df$x))$r.squared , 3) ,
                                 ", Sample Size is" , nrow(df)    ) )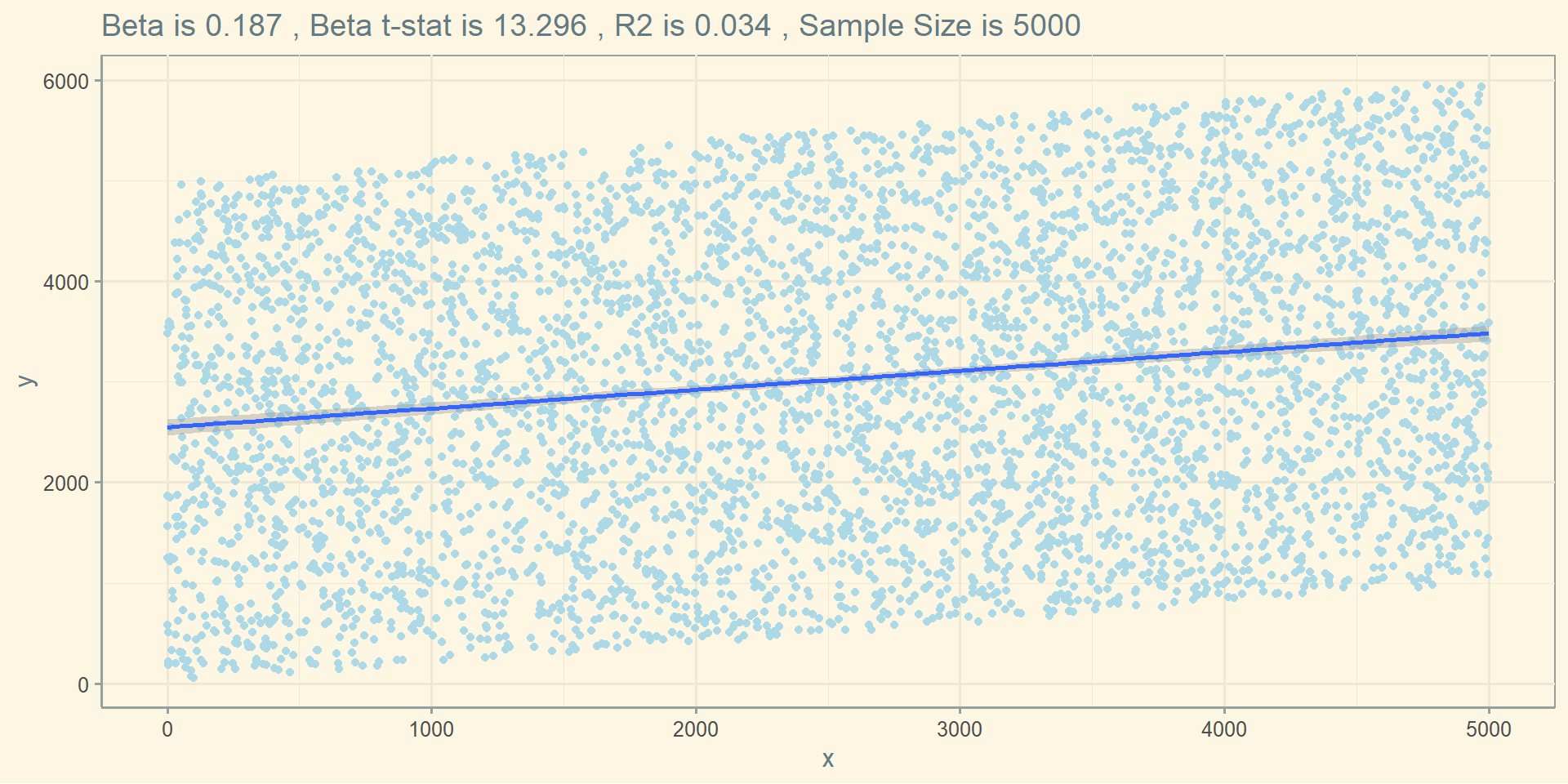

If you run a linear model using the sample you can observe, you might get this.

library(dplyr)
set.seed(1235)
random <- sample_n(df, sample)
reg <- lm(random$y ~ random$x)
sum <- summary(reg)
ggplot(df) +  geom_point( aes(x=x, y=y), color = "grey") +
              geom_point( data = random, aes(x=x, y=y) , color = "blue") +
              geom_smooth(data = random, aes(x=x, y=y) , method = lm) + 
              theme_solarized() + 
              labs(title = paste("Beta is" , round(reg$coefficients["random$x"], 3) , 
                                 ", Beta t-stat is" , round(summary(reg)$coefficients[2 , 3]   , 3) , 
                                 ", R2 is" , round(summary(reg)$r.squared , 3) ,
                                 ", Sample Size is" , nrow(random)    ) )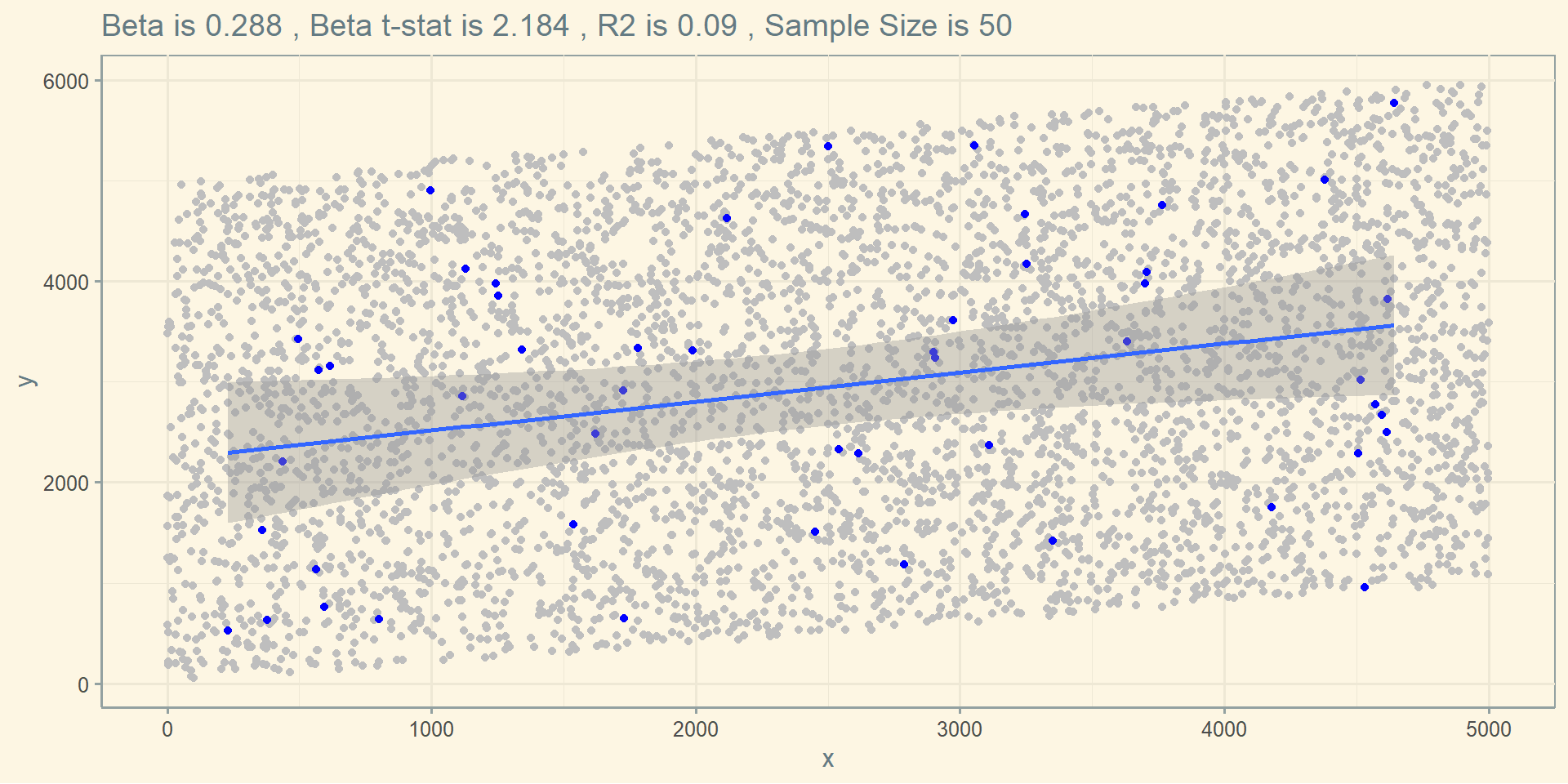

Or maybe this:

set.seed(1242)
random <- sample_n(df, sample)
reg <- lm(random$y ~ random$x)
sum <- summary(reg)
ggplot(df) +  geom_point( aes(x=x, y=y), color = "grey") +
              geom_point( data = random, aes(x=x, y=y) , color = "blue") +
              geom_smooth(data = random, aes(x=x, y=y) , method = lm) + 
              theme_solarized() + 
              labs(title = paste("Beta is" , round(reg$coefficients["random$x"], 3) , 
                                 ", Beta t-stat is" , round(summary(reg)$coefficients[2 , 3]   , 3) , 
                                 ", R2 is" , round(summary(reg)$r.squared , 3) ,
                                 ", Sample Size is" , nrow(random)    ) )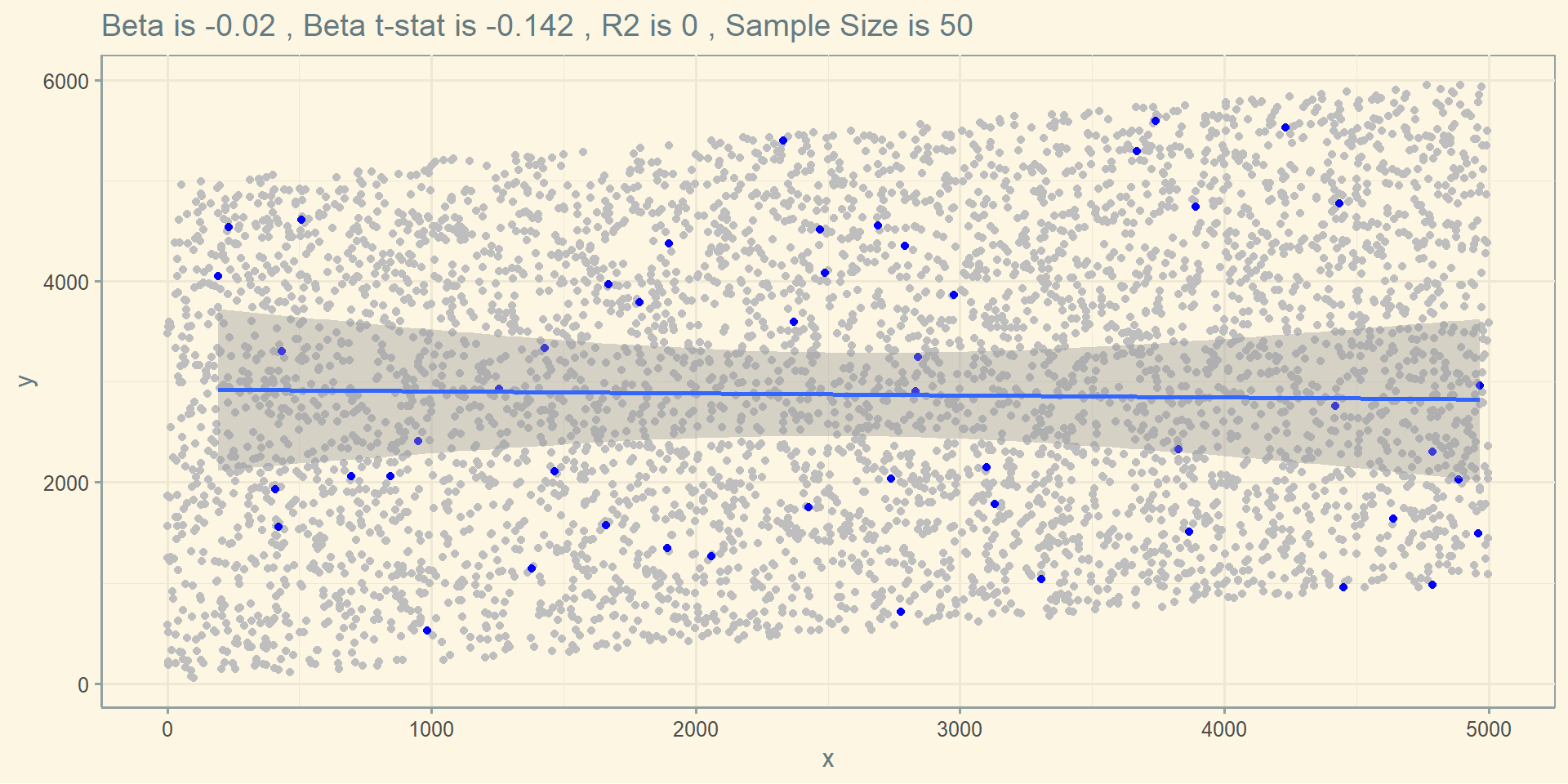

Or maybe this:

set.seed(1243)
random <- sample_n(df, sample)
reg <- lm(random$y ~ random$x)
sum <- summary(reg)
ggplot(df) +  geom_point( aes(x=x, y=y), color = "grey") +
              geom_point( data = random, aes(x=x, y=y) , color = "blue") +
              geom_smooth(data = random, aes(x=x, y=y) , method = lm) + 
              theme_solarized() + 
              labs(title = paste("Beta is" , round(reg$coefficients["random$x"], 3) , 
                                 ", Beta t-stat is" , round(summary(reg)$coefficients[2 , 3]   , 3) , 
                                 ", R2 is" , round(summary(reg)$r.squared , 3) ,
                                 ", Sample Size is" , nrow(random)    ) )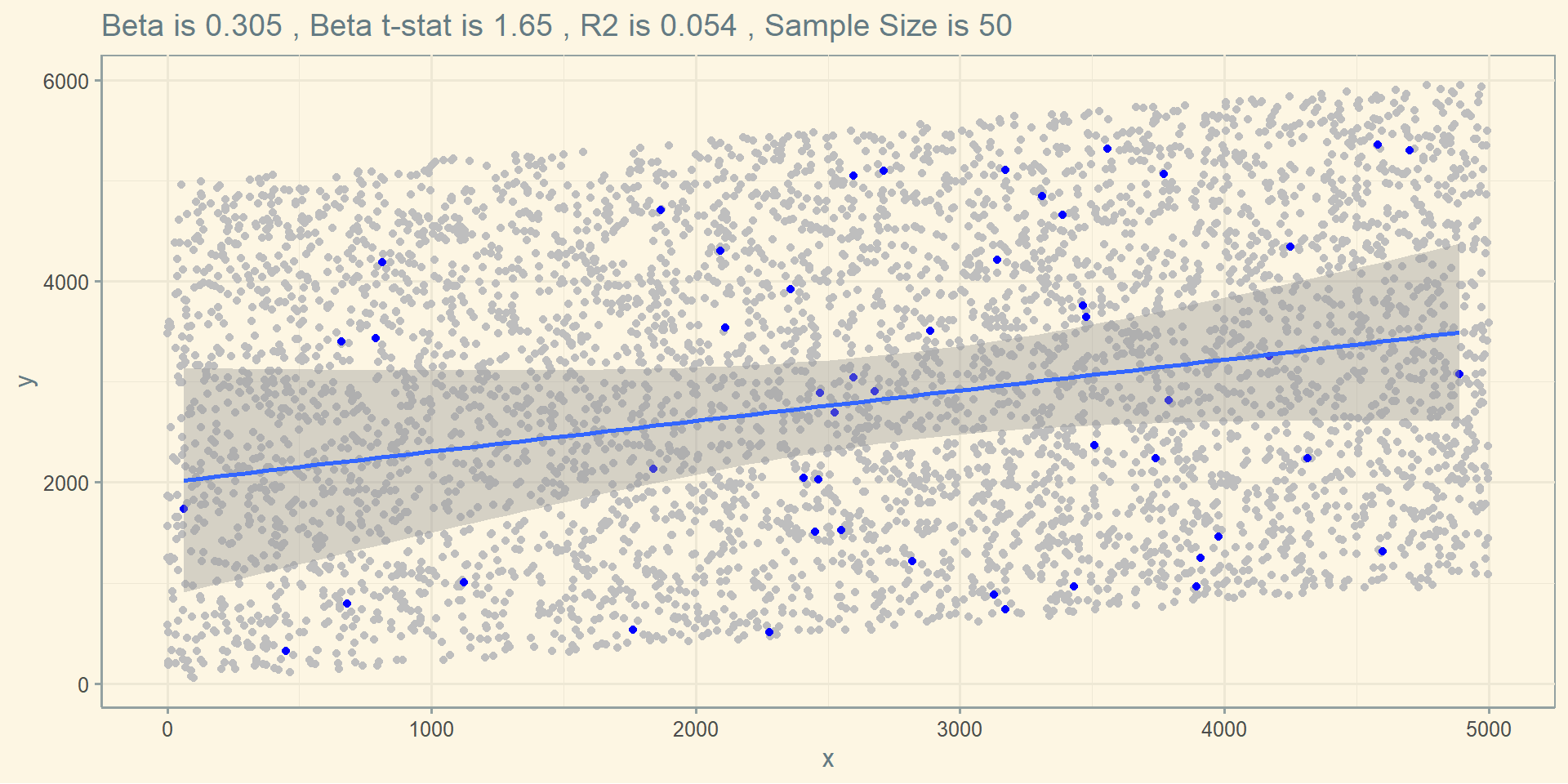

Or maybe several other estimates.

So, the takeaway is: always remember that you can only observe a sample of the population. If the sample you observe is biased, you will get biased estimates.

THANK YOU!

QUESTIONS?

Henrique C. Martins