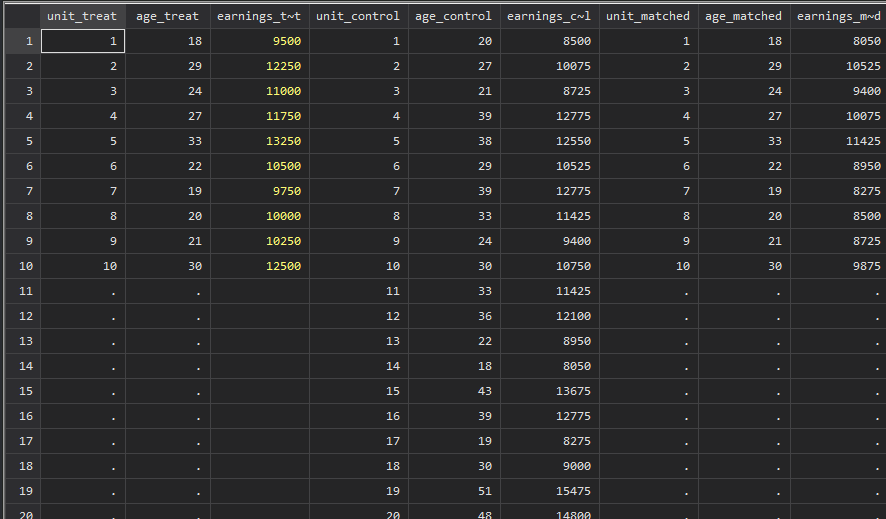
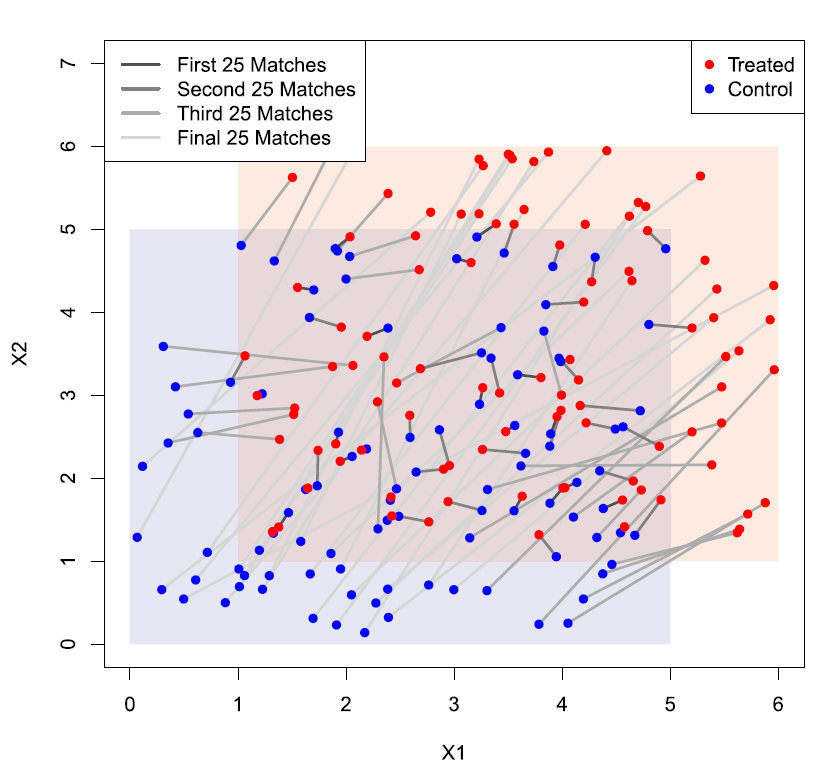
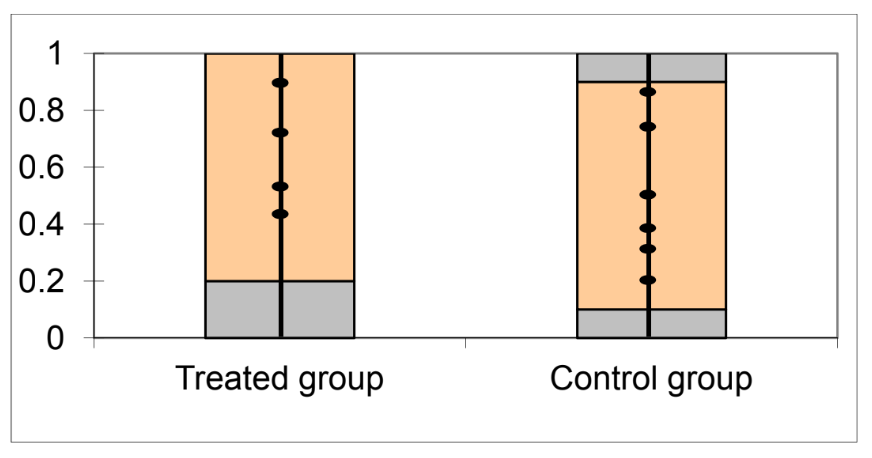
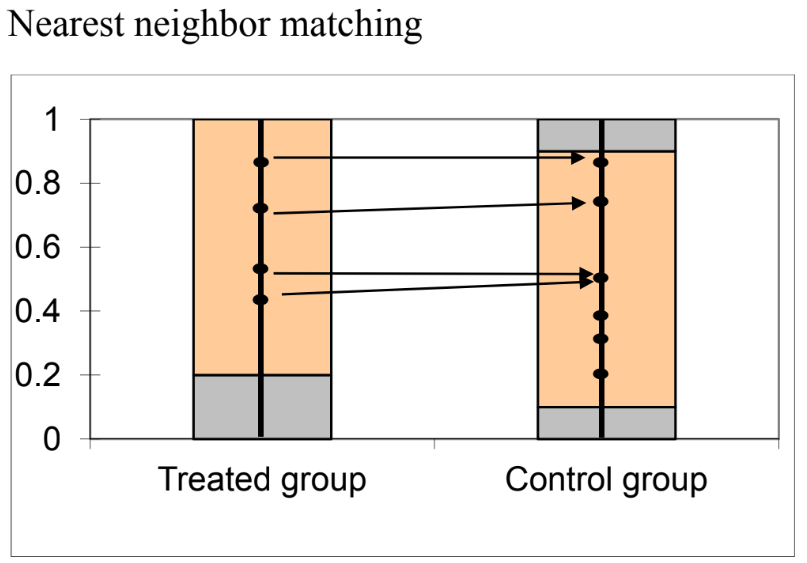
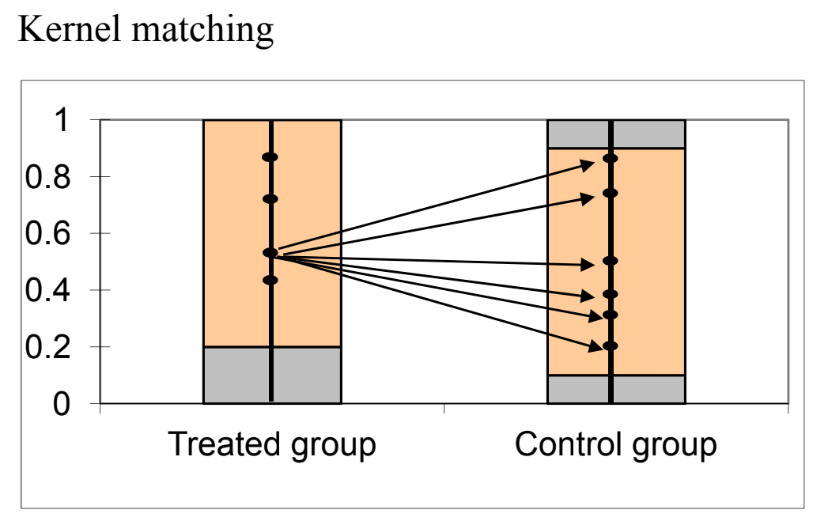
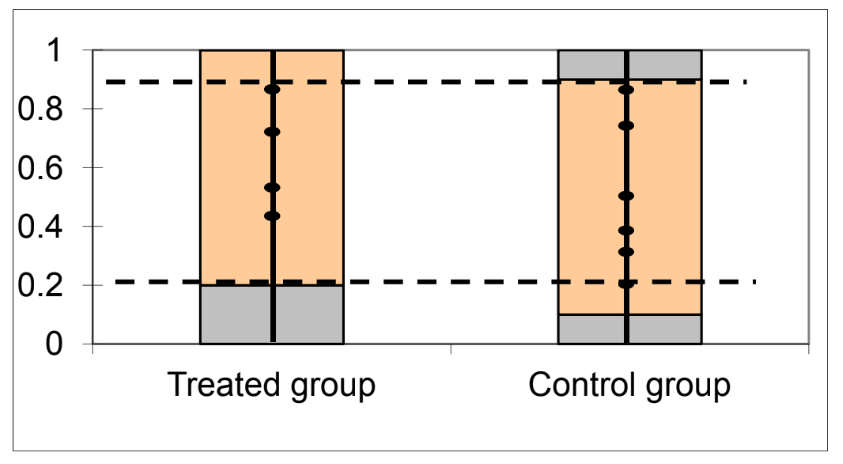
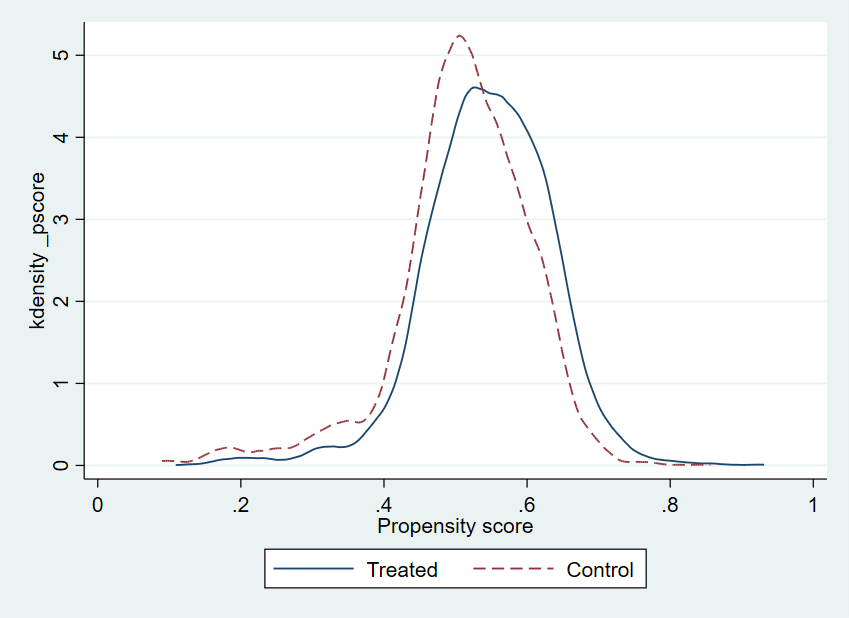
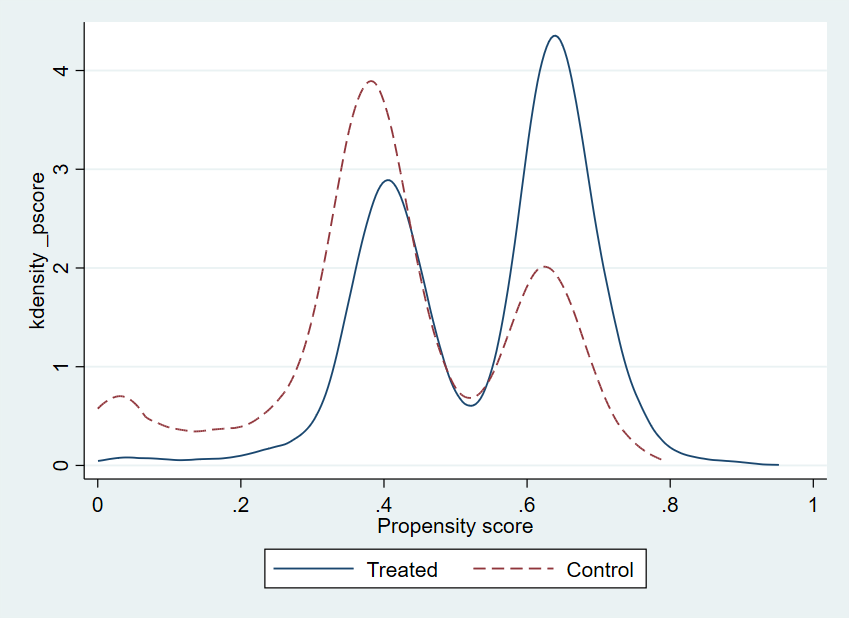
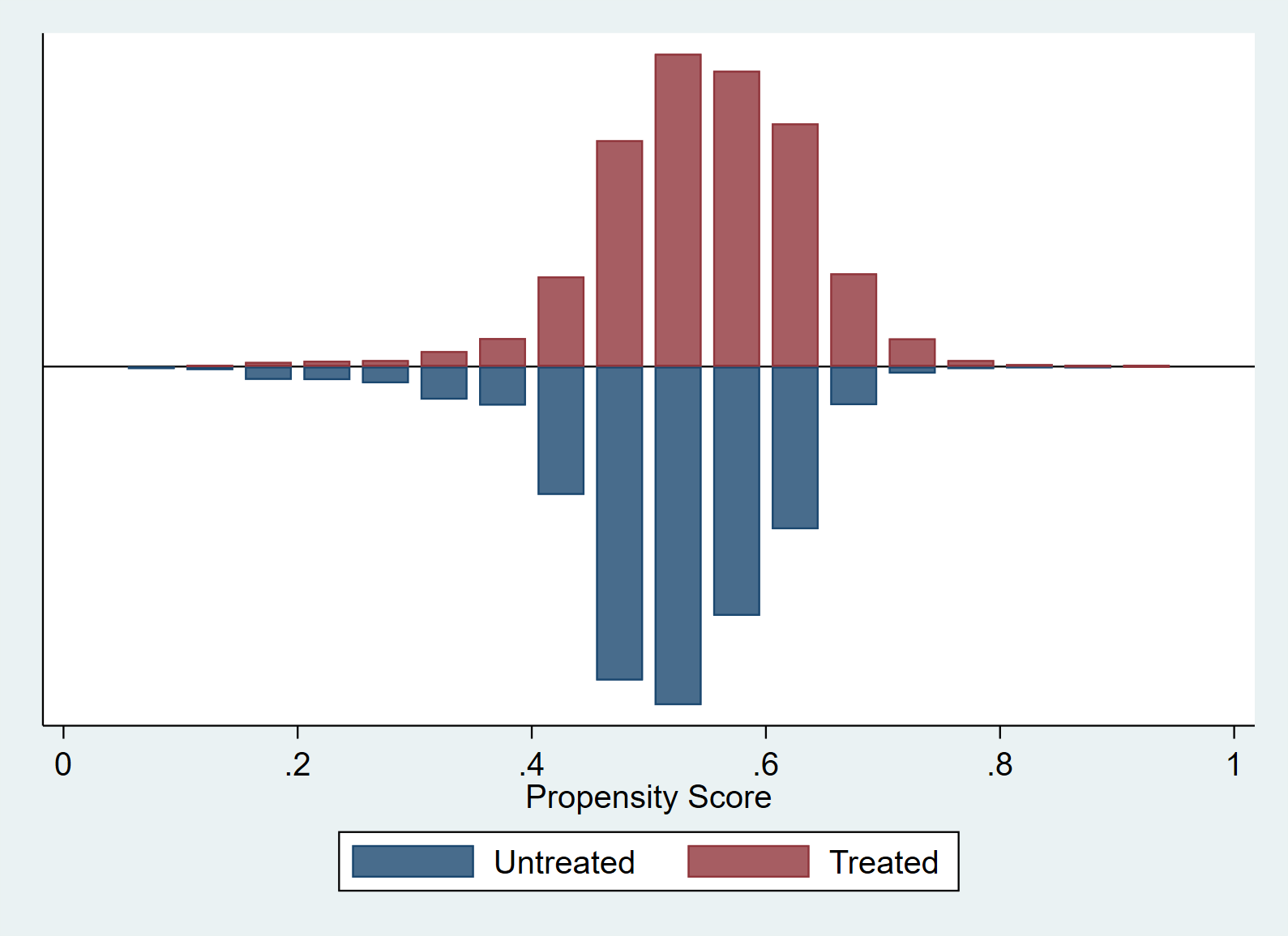
R
# Load necessary packages
library(tidyverse)
library(haven)
library(knitr)
library(kableExtra)
read_data <- function(df)
{
full_path <- paste("https://github.com/scunning1975/mixtape/raw/master/",df, sep = "")
df <- read_dta(full_path)
return(df)
}
training_example <- read_data("training_example.dta") %>% slice(1:20)
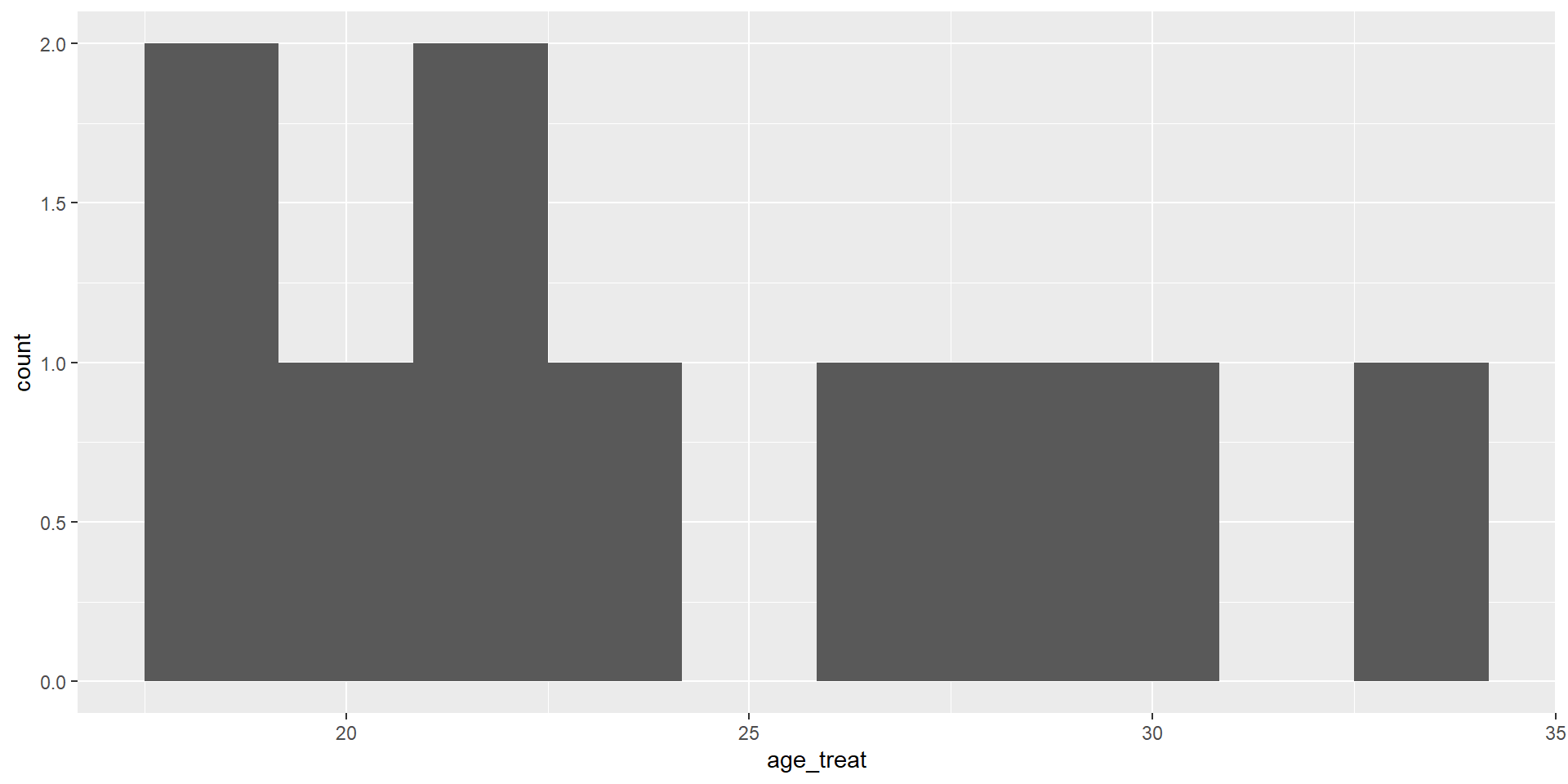
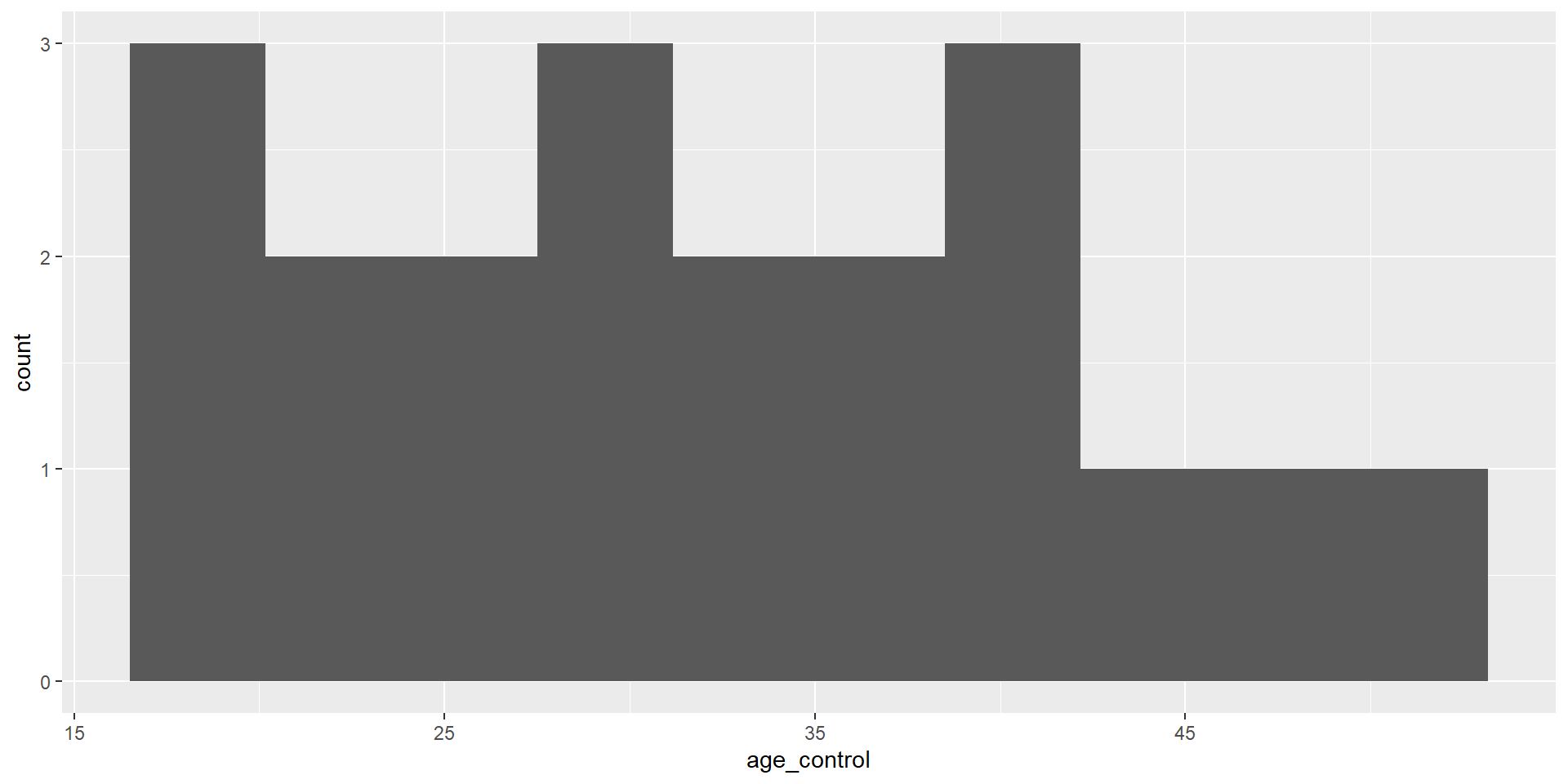
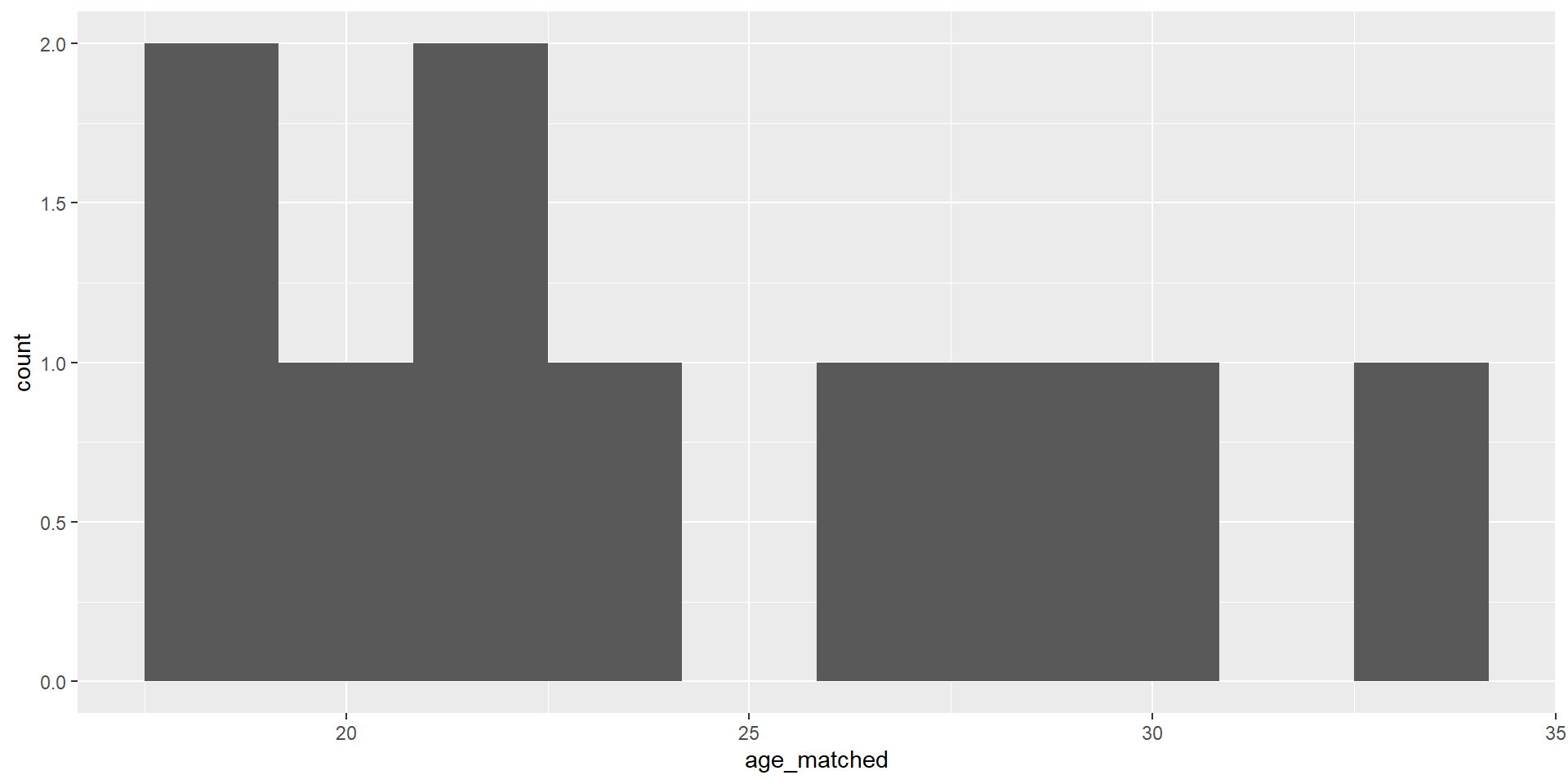
summary(training_example$age_treat) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
18.00 20.25 23.00 24.30 28.50 33.00 10 Min. 1st Qu. Median Mean 3rd Qu. Max.
18.00 23.50 31.50 31.95 39.00 51.00