Inferência Causal
Part 1
Agenda
Agenda
- Apresentação do syllabus do curso
- Apresentação dos critérios de avaliação
- Breve apresentação dos temas de pesquisa e discussão inicial sobre a entrega final
- Início do conteúdo
- Revisão
- Introdução a causalidade
Avaliação
Apresentação/Discussão de artigos: 25% (número de artigos a combinar)
Quizzes e exercícios: 30% (número aleatório, sem prévio aviso)
Projeto final de pesquisa: 35% (indicar tema até o 2o dia de aula)
Participação em aula: 10% (interações, perguntas, comentários, etc.)
(Nota para aprovação é >=6,0)
Sobre a letter
- Formato letter
- Entre 2k e 2.5k palavras a depender do journal.
The objective of a letter is to facilitate the rapid dissemination of important research that contains an insight, new data, or discuss current important topic.
Irá requerer todas as etapas da pesquisa (com ênfase na análise dos dados, i.e., regressões).
Idealmente, será submetida com o/a orientador/a. Leia-se, sua missão é “convencer” de que o trabalho final é submetível a uma revista.
Sobre a letter
Opções de revistas que aceitam letter (checar se referências e tabelas fazem parte do word count):
- Economic Letters (ABS3): 2k palavras
- Journal of Accounting and Public Policy (ABS3): 3k palavras
- Finance Research Letters (ABS2): 2.5k palavras
- Applied Economic Letters (ABS1): 2k palavras
- Brazilian Review of Finance (A4): 4k palavras
Você é bem-vindo/a para propor outro journal que aceite letter, sob condição de validação junto ao instrutor.
Sobre a letter
Em toda a aula, você fará o report da situação do seu documento em até 1 slide e em até 2 minutos.
Providenciar inclusão dos slides no monitor da sala no início da aula.
Stata
Providenciar programa instalado semana que vem.
Para instalação do Stata, seguir instruções da TI.
R
Providenciar programa instalado semana que vem.
Install R here Win
Install R here Mac
Install R Studio here
Para instalar e carregar os pacotes você precisa rodar as duas linhas abaixo.
Python
I might show some code in python, but I cannot offer you support on it.
Selection bias
Você nunca sabe o resultado do caminho que não toma.
Quais as aplicações do que vamos discutir?
Há uma série de questões de pesquisa que poderiam ser investigadas com as ferramentas que vamos discutir hoje.
Vale mais a pena estudar em escola particular ou pública?
Qual o efeito de investimentos de marketing têm na lucratividade?
Qual o efeito que jornadas de 4 dias semanais têm na produtividade?
Qual efeito que educação tem na remuneração futura?
E diversas outras semelhantes…
Antes de começar: Nossa agenda
Introdução a pesquisa quantitativa
Validade Externa vs. Validade Interna
Problemas em pesquisa quantitativa inferencial
Remédios
Introdução
O que fazemos em pesquisa quantitiva? Seguimos o método de pesquisa tradicional (com ajustes):
Observação
Questão de pesquisa
Modelo teórico (abstrato)
Hipóteses
Modelo empírico
Coleta de dados
Análise do resultado do modelo (diferente de análise de dados “pura”)
Conclusão/desdobramentos/aprendizados
Introdução
O que fazemos em pesquisa quantitiva? Seguimos o método de pesquisa tradicional (com ajustes):
Observação
Questão de pesquisa
Modelo teórico (abstrato): Aqui é onde a matemática é necessária
Hipóteses
Modelo empírico: Estatística e econometria necessárias
Coleta de dados: Geralmente secundários
Análise do resultado do modelo (diferente de análise de dados “pura”)
Conclusão/desdobramentos/aprendizados
Definição
Pesquisa quantitativa busca testar hipóteses…
…a partir da definição de modelos formais (abstratos)…
…de onde se estimam modelos empíricos utilizando a estatística e a econometria como mecanismos/instrumentos.
No fim do dia, buscamos entender as relações (que tenham validade interna e que ofereçam validade externa) entre diferentes variáveis de interesse.
Quais as vantagens?
- Validade externa:
- Conceito de que, se a pesquisa tem validade externa, os seus achados são representativos.
- I.e., são válidos além do seu modelo. Resultados “valem externamente”.
- Idealmente, buscamos resultados que valem externamente para acumular conhecimento…
- …naturalmente, nem toda pesquisa quantitativa oferece validade externa. A pesquisa ótima sim. A pesquisa excelente tem validade externa para além do seu tempo.
- Pesquisa qualitativa dificilmente oferece validade externa.
Quais as armadilhas?
- Validade interna:
- Conceito de que a pesquisa precisa de validade interna para que seus resultados sejam críveis.
- I.e., os resultados não podem conter erros, vieses, problemas de estimação, problemas nos dados, etc..
- É aqui que a gente separa a pesquisa ruim da pesquisa boa. Para ser levada a sério, a pesquisa PRECISA ter validade interna.
- Mas isso, nem sempre é trivial. Muitas pesquisas que vemos publicadas, mesmo em top journals, não têm validade interna (seja por erro do pesquisador, por método incorreto, por falta de dados…)
- Mas cada vez mais, avaliadores estão de olho em problemas e em modelos Trash-in-Trash-out
Como fazemos na prática?
Exemplo de modelo empírico:
\(Y_{i} = α + 𝜷_{1} × X_i + Controls + error\)
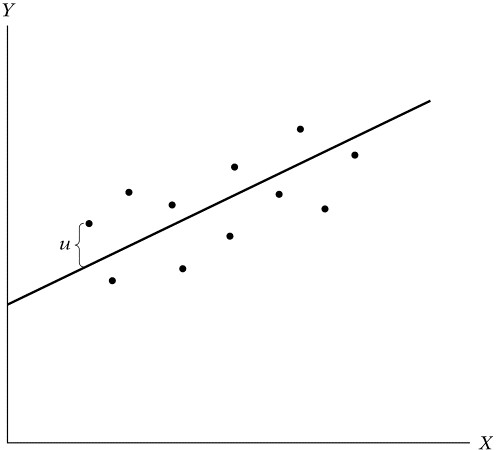
Uma vez que estimemos esse modelo, temos o valor, o sinal e a significância do \(𝜷\).
Se o Beta for significativamente diferente de zero e positivo –> X e Y estão positivamente correlacionados.
O problema? Os pacotes estatísticos que utilizamos sempre “cospem” um beta. Seja ele com ou sem viés.
Cabe ao pesquisador ter um design empírico que garanta que o beta estimado tenha validade interna.
Como fazemos na prática?
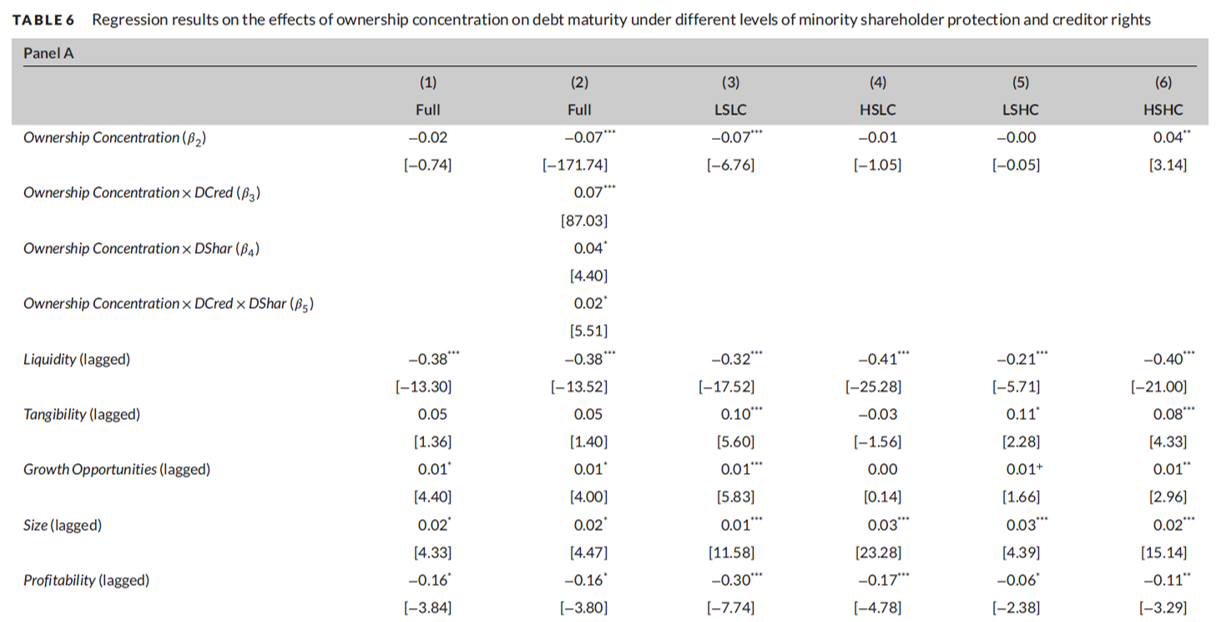
A decisão final é baseada na significância do Beta estimado. Se significativo, as variáveis são relacionadas e fazemos inferências em cima disso.
Contudo, sem um design empírico inteligente, o beta encontrado pode ter literalmente qualquer sinal e significância.
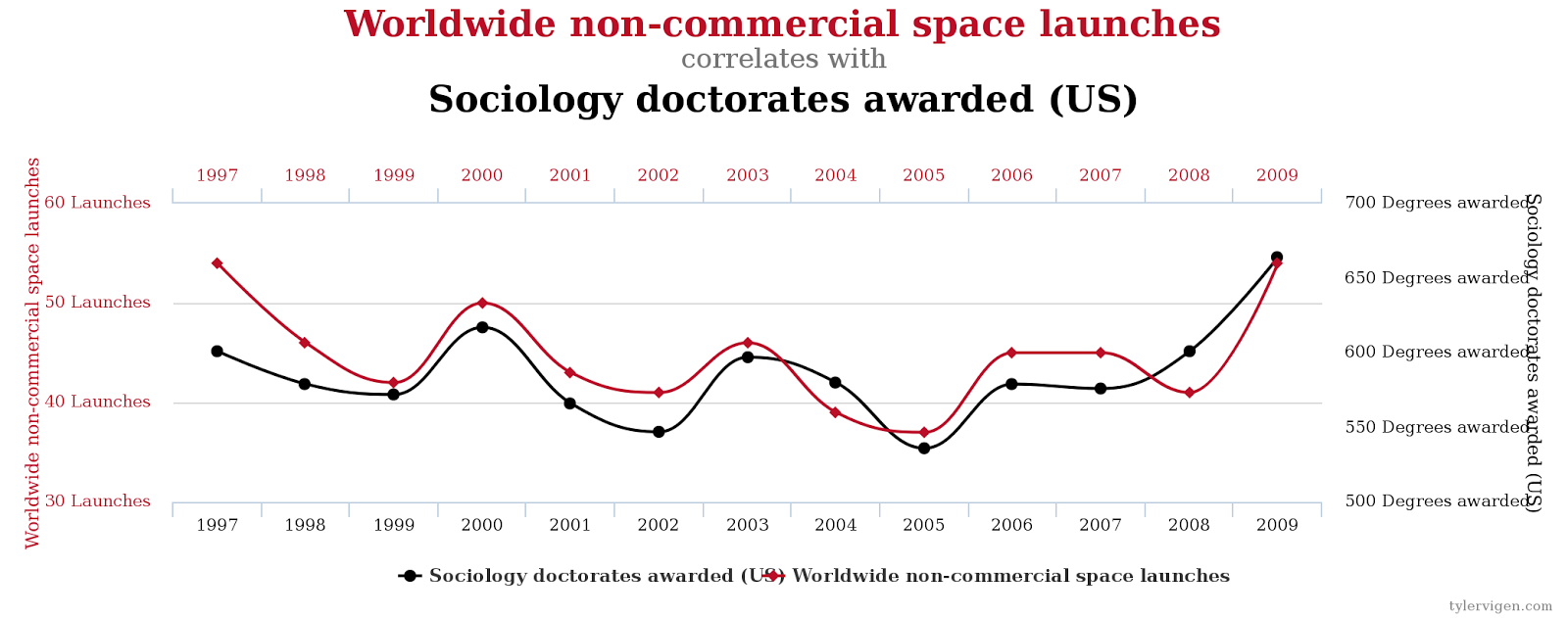
Exemplo desses problemas
Veja esse site.
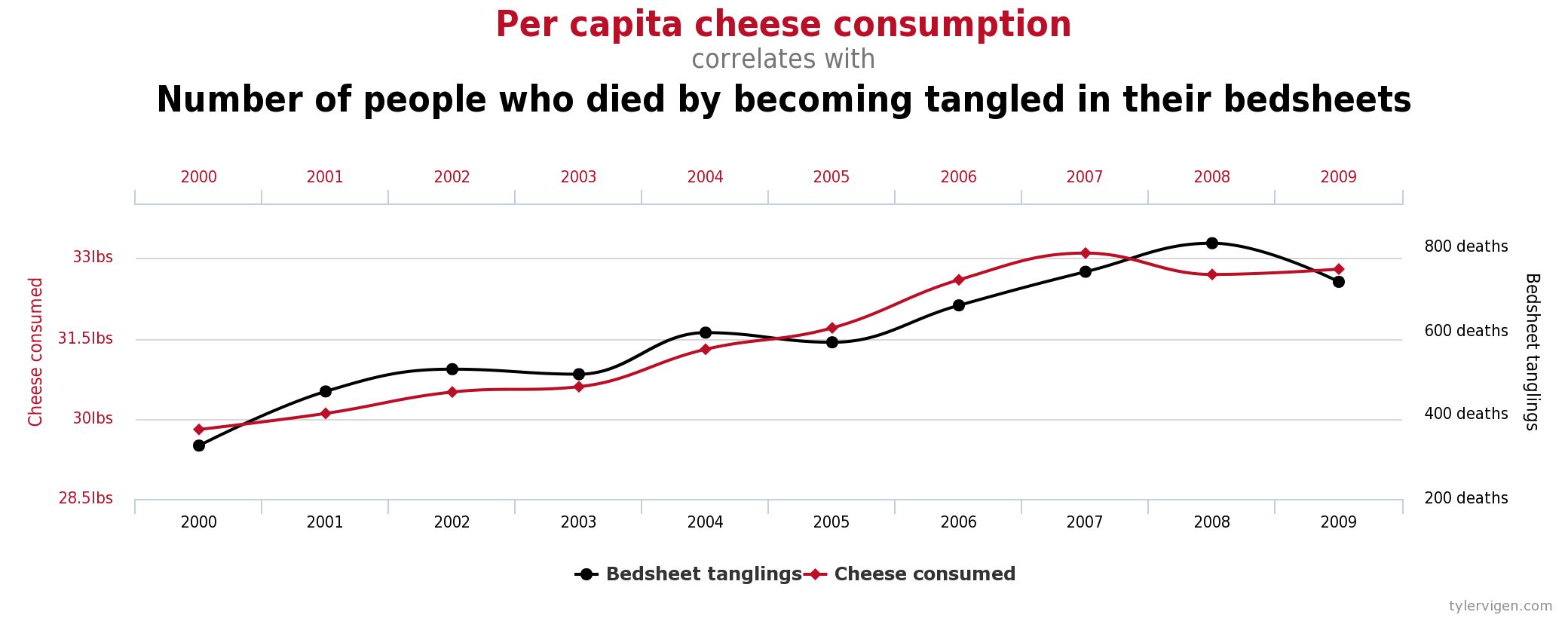
Exemplo desses problemas
Veja esse site.
Selection bias - We see I
R
library(data.table)
library(ggplot2)
# Generate Data
n = 10000
set.seed(100)
x <- rnorm(n)
y <- rnorm(n)
data1 <- 1/(1+exp( 2 - x - y))
group <- rbinom(n, 1, data1)
# Data Together
data_we_see <- subset(data.table(x, y, group), group==1)
data_all <- data.table(x, y, group)
# Graphs
ggplot(data_we_see, aes(x = x, y = y)) +
geom_point(aes(colour = factor(-group)), size = 1) +
geom_smooth(method=lm, se=FALSE, fullrange=FALSE)+
labs( y = "", x="", title = "The observations we see")+
xlim(-3,4)+ ylim(-3,4)+
theme(plot.title = element_text(color="black", size=30, face="bold"),
panel.background = element_rect(fill = "grey95", colour = "grey95"),
axis.text.y = element_text(face="bold", color="black", size = 18),
axis.text.x = element_text(face="bold", color="black", size = 18),
legend.position = "none")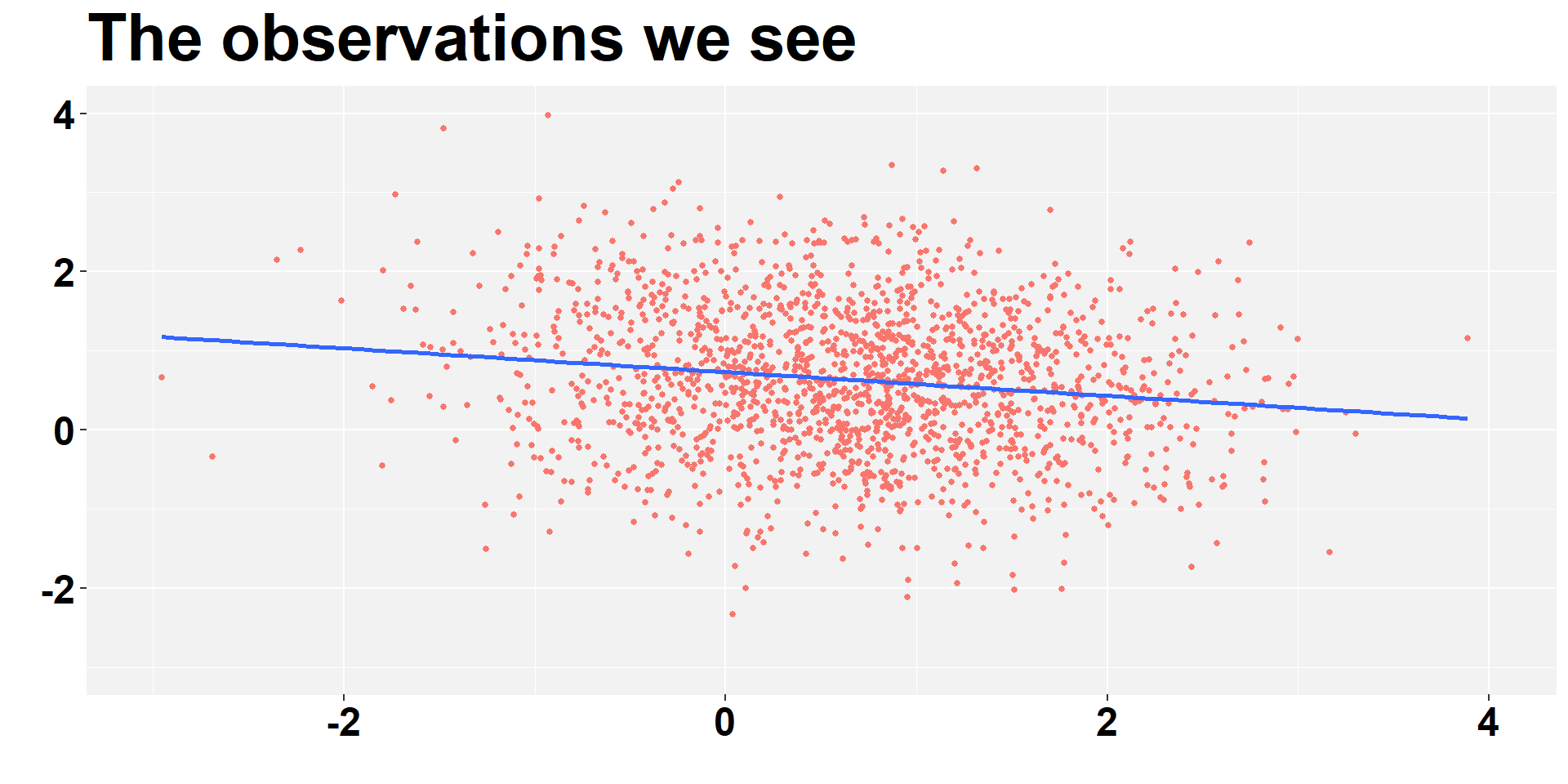
Python
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
n = 10000
np.random.seed(100)
x = np.random.normal(size=n)
y = np.random.normal(size=n)
data1 = 1 / (1 + np.exp(2 - x - y))
group = np.random.binomial(1, data1, n)
data_we_see = pd.DataFrame({'x': x[group == 1], 'y': y[group == 1], 'group': group[group == 1]})
data_all = pd.DataFrame({'x': x, 'y': y, 'group': group})
sns.set(style='whitegrid')
plt.figure(figsize=(7, 5))
plt.scatter(data_we_see['x'], data_we_see['y'], c=-data_we_see['group'], cmap='viridis', s=20)
sns.regplot(x='x', y='y', data=data_we_see, scatter=False, ci=None, line_kws={'color': 'blue'})
plt.title("The observations we see", fontsize=18)
plt.xlabel("")
plt.ylabel("")
plt.show()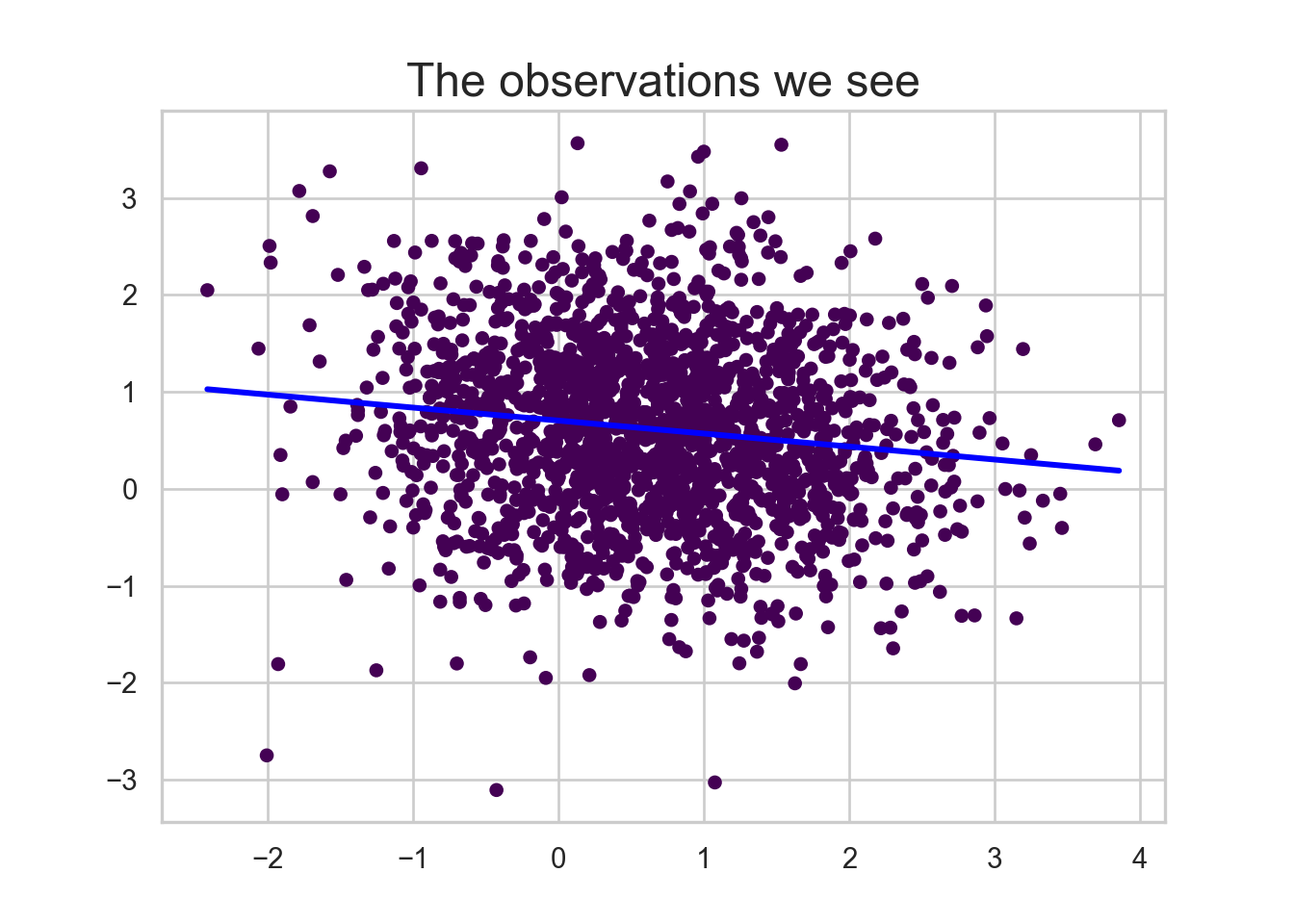
Stata
clear all
set seed 100
set obs 10000
gen x = rnormal(0,1)
gen y = rnormal(0,1)
gen data1 = 1 / (1 + exp(2 - x - y))
gen group = rbinomial(1, data1)
twoway (scatter x y if group == 1, mcolor(black) msize(small)) (lfit y x if group == 1, color(blue)),title("The observations we see", size(large) ) xtitle("") ytitle("")
quietly graph export figs/graph1.svg, replace
Selection bias - We see II
R
Call:
lm(formula = y ~ x, data = data_we_see)
Residuals:
Min 1Q Median 3Q Max
-3.05878 -0.63754 -0.00276 0.62056 3.11374
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.72820 0.02660 27.37 < 2e-16 ***
x -0.14773 0.02327 -6.35 2.75e-10 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.9113 on 1747 degrees of freedom
Multiple R-squared: 0.02256, Adjusted R-squared: 0.022
F-statistic: 40.32 on 1 and 1747 DF, p-value: 2.746e-10Python
import statsmodels.api as sm
import pandas as pd
n = 10000
np.random.seed(100)
x = np.random.normal(size=n)
y = np.random.normal(size=n)
data1 = 1 / (1 + np.exp(2 - x - y))
group = np.random.binomial(1, data1, n)
data_we_see = pd.DataFrame({'x': x[group == 1], 'y': y[group == 1], 'group': group[group == 1]})
data_all = pd.DataFrame({'x': x, 'y': y, 'group': group})
X = data_we_see['x']
X = sm.add_constant(X)
y = data_we_see['y']
model = sm.OLS(y, X).fit()
print(model.summary()) OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.018
Model: OLS Adj. R-squared: 0.018
Method: Least Squares F-statistic: 33.84
Date: ter, 30 jan 2024 Prob (F-statistic): 7.06e-09
Time: 15:38:24 Log-Likelihood: -2411.1
No. Observations: 1809 AIC: 4826.
Df Residuals: 1807 BIC: 4837.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 0.7037 0.026 26.826 0.000 0.652 0.755
x -0.1339 0.023 -5.817 0.000 -0.179 -0.089
==============================================================================
Omnibus: 4.656 Durbin-Watson: 1.973
Prob(Omnibus): 0.097 Jarque-Bera (JB): 5.264
Skew: -0.038 Prob(JB): 0.0720
Kurtosis: 3.253 Cond. No. 1.93
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.Stata
Number of observations (_N) was 0, now 10,000.
Source | SS df MS Number of obs = 1,872
-------------+---------------------------------- F(1, 1870) = 48.62
Model | 40.9398907 1 40.9398907 Prob > F = 0.0000
Residual | 1574.57172 1,870 .842016963 R-squared = 0.0253
-------------+---------------------------------- Adj R-squared = 0.0248
Total | 1615.51161 1,871 .863448215 Root MSE = .91761
------------------------------------------------------------------------------
y | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
x | -.1579538 .0226526 -6.97 0.000 -.2023808 -.1135269
_cons | .7202285 .0257215 28.00 0.000 .6697827 .7706744
------------------------------------------------------------------------------Selection bias - All I
R
ggplot(data_all, aes(x = x, y = y, colour=group)) +
geom_point(aes(colour = factor(-group)), size = 1) +
geom_smooth(method=lm, se=FALSE, fullrange=FALSE)+
labs( y = "", x="", title = "All observations")+
xlim(-3,4)+ ylim(-3,4)+
theme(plot.title = element_text(color="black", size=30, face="bold"),
panel.background = element_rect(fill = "grey95", colour = "grey95"),
axis.text.y = element_text(face="bold", color="black", size = 18),
axis.text.x = element_text(face="bold", color="black", size = 18),
legend.position = "none")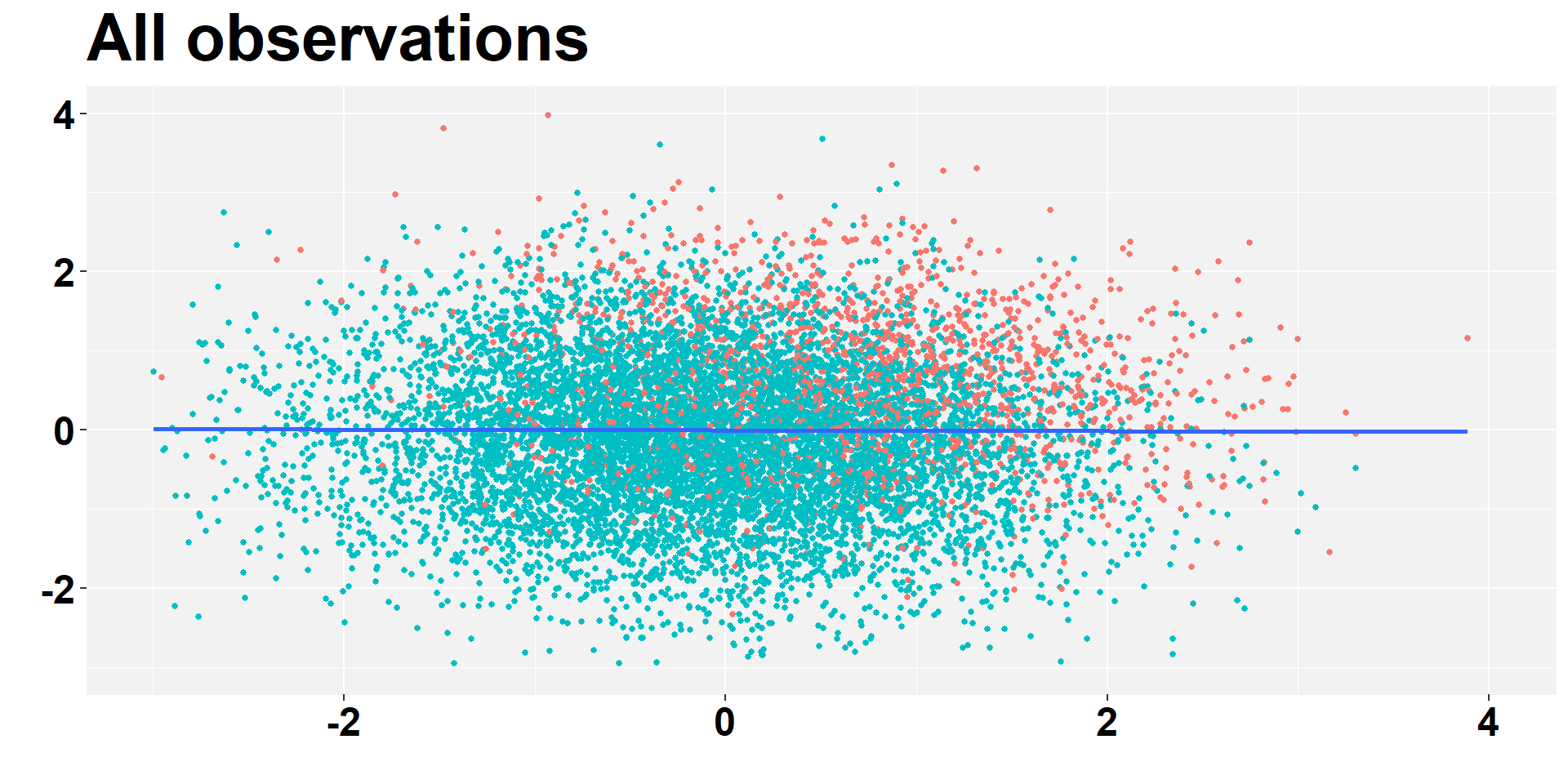
Python
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
sns.set(style='whitegrid')
plt.figure(figsize=(6, 4))
sns.scatterplot(data=data_all, x='x', y='y', hue='group', palette=['blue', 'red'], s=20)
sns.regplot(data=data_all, x='x', y='y', scatter=False, ci=None, line_kws={'color': 'blue'})
plt.title("All observations", fontsize=18)
plt.xlabel("")
plt.ylabel("")
plt.legend(title="Group", labels=["0", "1"], loc="upper left")
plt.gca().get_legend().remove()
plt.show()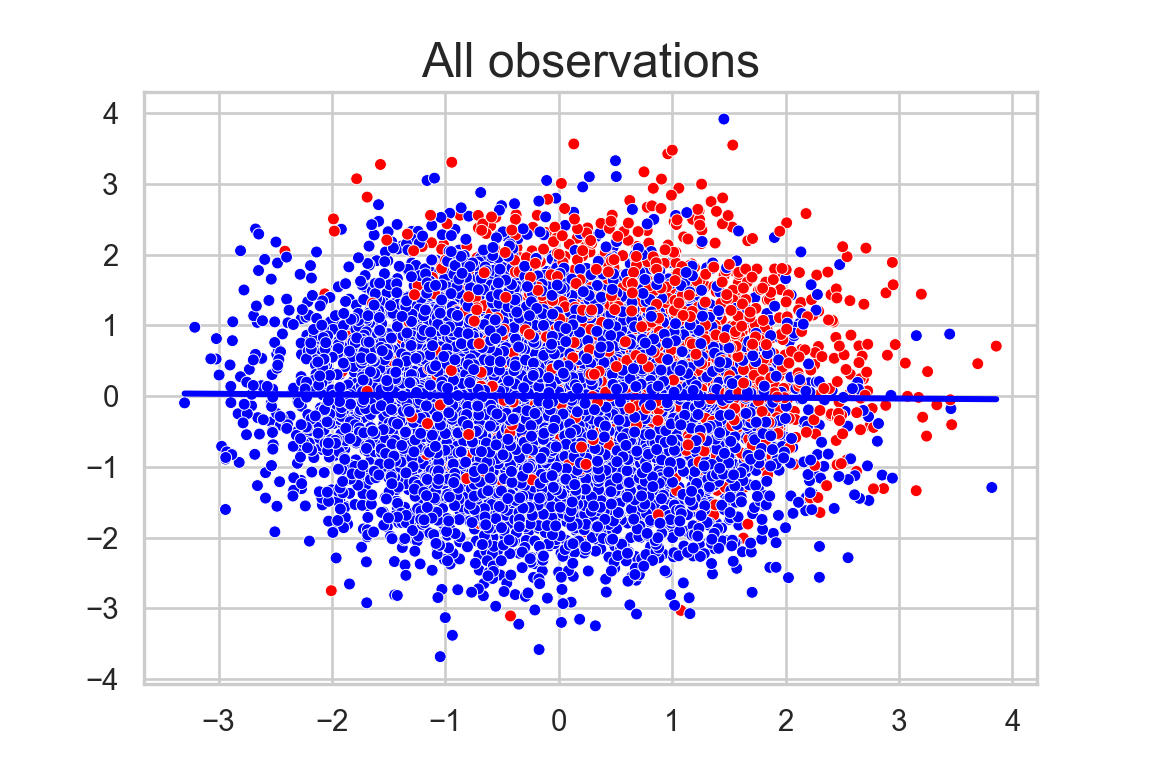
Number of observations (_N) was 0, now 10,000.
Selection bias - All I
Call:
lm(formula = y ~ x, data = data_all)
Residuals:
Min 1Q Median 3Q Max
-3.9515 -0.6716 0.0087 0.6698 3.9878
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.011825 0.009994 -1.183 0.237
x -0.003681 0.010048 -0.366 0.714
Residual standard error: 0.9994 on 9998 degrees of freedom
Multiple R-squared: 1.342e-05, Adjusted R-squared: -8.66e-05
F-statistic: 0.1342 on 1 and 9998 DF, p-value: 0.7141Python
import statsmodels.api as sm
import pandas as pd
n = 10000
np.random.seed(100)
x = np.random.normal(size=n)
y = np.random.normal(size=n)
data1 = 1 / (1 + np.exp(2 - x - y))
group = np.random.binomial(1, data1, n)
data_we_see = pd.DataFrame({'x': x[group == 1], 'y': y[group == 1], 'group': group[group == 1]})
data_all = pd.DataFrame({'x': x, 'y': y, 'group': group})
X = data_all['x']
X = sm.add_constant(X)
y = data_all['y']
model = sm.OLS(y, X).fit()
print(model.summary()) OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.000
Model: OLS Adj. R-squared: 0.000
Method: Least Squares F-statistic: 1.281
Date: ter, 30 jan 2024 Prob (F-statistic): 0.258
Time: 15:38:32 Log-Likelihood: -14157.
No. Observations: 10000 AIC: 2.832e+04
Df Residuals: 9998 BIC: 2.833e+04
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const -0.0003 0.010 -0.034 0.973 -0.020 0.019
x -0.0112 0.010 -1.132 0.258 -0.031 0.008
==============================================================================
Omnibus: 0.267 Durbin-Watson: 2.009
Prob(Omnibus): 0.875 Jarque-Bera (JB): 0.242
Skew: 0.009 Prob(JB): 0.886
Kurtosis: 3.017 Cond. No. 1.01
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.Stata
Number of observations (_N) was 0, now 10,000.
Source | SS df MS Number of obs = 10,000
-------------+---------------------------------- F(1, 9998) = 0.28
Model | .284496142 1 .284496142 Prob > F = 0.5938
Residual | 9999.04347 9,998 1.00010437 R-squared = 0.0000
-------------+---------------------------------- Adj R-squared = -0.0001
Total | 9999.32797 9,999 1.0000328 Root MSE = 1.0001
------------------------------------------------------------------------------
y | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
x | -.0053101 .009956 -0.53 0.594 -.0248259 .0142057
_cons | .0006182 .0100006 0.06 0.951 -.0189849 .0202213
------------------------------------------------------------------------------Selection bias
Selection bias não é o único dos nossos problemas, mas é um importante.
Veja que suas conclusões mudaram significativamente.
Não seria difícil criar um exemplo em que o coeficiente verdadeiro fosse positivo.
Exemplo desses problemas
Source: Angrist
Não podemos pegar dois caminhos.
Exemplo desses problemas
Source: Angrist
Não podemos comparar pessoas que não são comparáveis.
O que precisamos fazer?
Definir um bom Design empírico
No mundo ideal: teríamos universos paralelos. Teríamos dois clones, em que cada um escolhe um caminho. Todo o resto é igual.
- Obviamente, isso não existe.
Segunda melhor solução: experimentos
Mas o que é um experimento?
Grupo de tratamento vs. Grupo de controle
Igualdade entre os grupos (i.e., aleatoriedade no sampling)
- Nada diferencia os grupos a não ser o fato de que um indivíduo recebe tratamento e o outro não
- Estamos comparando maças com maças e laranjas com laranjas
Testes placebo/falsificação.
The challenge
Correlation & Causality
It is very common these days to hear someone say “correlation does not mean causality.”
In essence, that is true.
- The killer struck during daylight. Had the sun not been out that day, the victim would have been safe.
- There is a correlation, but it is clear there is no causation.
Correlation & Causality
Sometimes, there is causality even when we do not observe correlation.
The sailor is adjusting the rudder on a windy day to align the boat with the wind, but the boat is not changing direction. (Source: The Mixtape)
In this example, the sailor is endogenously adjusting the course to balance the unobserved wind.
The challenge
- I will discuss some issues in using plain OLS models in Finance Research (mainly with panel data).
- I will avoid the word “endogeneity” as much as I can
- I will also avoid the word “identification” because identification does not guarantee causality and vice-versa (Kahn and Whited 2017)
- The discussion is based on Atanasov and Black (2016)
The challenge
Imagine that you want to investigate the effect of Governance on Q
- You may have more covariates explaining Q (omitted from slides)
\(𝑸_{i} = α + 𝜷_{i} × Gov + Controls + error\)
All the issues in the next slides will make it not possible to infer that changing Gov will CAUSE a change in Q
That is, cannot infer causality
1) Reverse causation
One source of bias is: reverse causation
Perhaps it is Q that causes Gov
OLS based methods do not tell the difference between these two betas:
\(𝑄_{i} = α + 𝜷_{i} × Gov + Controls + error\)
\(Gov_{i} = α + 𝜷_{i} × Q + Controls + error\)
If one Beta is significant, the other will most likely be significant too
You need a sound theory!
2) Omitted variable bias (OVB)
The second source of bias is: OVB
Imagine that you do not include an important “true” predictor of Q
Let’s say, long is: \(𝑸_{i} = 𝜶_{long} + 𝜷_{long}* gov_{i} + δ * omitted + error\)
But you estimate short: \(𝑸_{i} = 𝜶_{short} + 𝜷_{short}* gov_{i} + error\)
\(𝜷_{short}\) will be:
\(𝜷_{short} = 𝜷_{long}\) + bias
\(𝜷_{short} = 𝜷_{long}\) + relationship between omitted (omitted) and included (Gov) * effect of omitted in long (δ)
- Where: relationship between omitted (omitted) and included (Gov) is: \(Omitted = 𝜶 + ϕ *gov_{i} + u\)
Thus, OVB is: \(𝜷_{short} – 𝜷_{long} = ϕ * δ\)
3) Specification error
The third source of bias is: Specification error
Even if we could perfectly measure gov and all relevant covariates, we would not know for sure the functional form through which each influences q
- Functional form: linear? Quadratic? Log-log? Semi-log?
Misspecification of x’s is similar to OVB
4) Signaling
The fourth source of bias is: Signaling
Perhaps, some individuals are signaling the existence of an X without truly having it:
- For instance: firms signaling they have good governance without having it
This is similar to the OVB because you cannot observe the full story
5) Simultaneity
The fifth source of bias is: Simultaneity
Perhaps gov and some other variable x are determined simultaneously
Perhaps there is bidirectional causation, with q causing gov and gov also causing q
In both cases, OLS regression will provide a biased estimate of the effect
Also, the sign might be wrong
6) Heterogeneous effects
The sixth source of bias is: Heterogeneous effects
Maybe the causal effect of gov on q depends on observed and unobserved firm characteristics:
- Let’s assume that firms seek to maximize q
- Different firms have different optimal gov
- Firms know their optimal gov
- If we observed all factors that affect q, each firm would be at its own optimum and OLS regression would give a non-significant coefficient
In such case, we may find a positive or negative relationship.
Neither is the true causal relationship
7) Construct validity
The seventh source of bias is: Construct validity
Some constructs (e.g. Corporate governance) are complex, and sometimes have conflicting mechanisms
We usually don’t know for sure what “good” governance is, for instance
It is common that we use imperfect proxies
They may poorly fit the underlying concept
8) Measurement error
The eighth source of bias is: Measurement error
“Classical” random measurement error for the outcome will inflate standard errors but will not lead to biased coefficients.
- \(y^{*} = y + \sigma_{1}\)
- If you estimante \(y^{*} = f(x)\), you have \(y + \sigma_{1} = x + \epsilon\)
- \(y = x + u\)
- where \(u = \epsilon + \sigma_{1}\)
“Classical” random measurement error in x’s will bias coefficient estimates toward zero
- \(x^{*} = x + \sigma_{2}\)
- Imagine that \(x^{*}\) is a bunch of noise
- It would not explain anything
- Thus, your results are biased toward zero
9) Observation bias
The ninth source of bias is: Observation bias
This is analogous to the Hawthorne effect, in which observed subjects behave differently because they are observed
Firms which change gov may behave differently because their managers or employees think the change in gov matters, when in fact it has no direct effect
10) Interdependent effects
The tenth source of bias is: Interdependent effects
Imagine that a governance reform that will not affect share prices for a single firm might be effective if several firms adopt
Conversely, a reform that improves efficiency for a single firm might not improve profitability if adopted widely because the gains will be competed away
“One swallow doesn’t make a summer”
11) Selection bias
The eleventh source of bias is: Selection bias
If you run a regression with two types of companies
- High gov (let’s say they are the treated group)
- Low gov (let’s say they are the control group)
Without any matching method, these companies are likely not comparable
Thus, the estimated beta will contain selection bias
The bias can be either be positive or negative
It is similar to OVB
12) Self-Selection
The twelfth source of bias is: Self-Selection
Self-selection is a type of selection bias
Usually, firms decide which level of governance they adopt
There are reasons why firms adopt high governance
- If observable, you need to control for
- If unobservable, you have a problem
It is like they “self-select” into the treatment.
- Units decide whether they receive the treatment of not
Your coefficients will be biased.
Conclusão
Pesquisa quantitativa tem a parte quanti (métodos, modelos, etc.)…
… Mas talvez a parte mais importante seja o desenho da pesquisa (design empírico)!
Preocupações recentes em pesquisa
P-Hacking
Artigo original aqui.
Preocupações recentes em pesquisa
Publication bias
Artigo original aqui.
Preocupações recentes em pesquisa
Crise de replicação
Artigo original aqui.
Some fun stuff
Some fun stuff
Some fun stuff
Some fun stuff
Some fun stuff
Conterfactuals
Conterfactuals
Imagine that John and Mary are moving to the north of Canada.
John has a history of respiratory disease and decide to buy insurance.
Mary does not have a history of respiratory disease and decide not to buy insurance.
What is the causal effect of buying insurance?
| Default | John | Mary |
|---|---|---|
| State of insurance | 1 | 0 |
| Situation without insurance | n.o. |
5 |
| Situation with insurance | 4 | n.o. |
| Observed | 4 | 5 |
| Effect | ? | ? |
Conterfactuals
Naïve calculation: comparing John com Mary
\[Y_{john} - Y_{Mary} = 4 - 5 = -1\]
Conclusion: buying insurance has a negative effect on health.
This is wrong!
Conterfactuals
| Default | John | Mary |
|---|---|---|
| State of insurance | 1 | 0 |
| Situation without insurance | 3 |
5 |
| Situation with insurance | 4 | 5 |
| Observed | 4 | 5 |
| Effect | ? | ? |
\[(Y_{1,john} - Y_{0,john}) + (Y_{1,Mary}- Y_{0,Mary}) = 4 - 3 + 5 - 5 = 0.5\]
Conclusion: buying insurance has a positive effect of 1 in John’s health and average effect of 0.5 in the sample’s health (i.e. averages conditional on insurance status).
Regressions
Regression Source: Mastering Metrics
Let’s see how a regression could solve the problem. Imagine that you have the following data on students’ application. (Decisions in bold)
| Student | Private | Private | Private | Public | Public | Public | Earnings |
|---|---|---|---|---|---|---|---|
| Ivy | Leafy | Smart | State | Tall | Altered | 110,000 | |
| 1 | Reject | Admit | Admit | 110,000 | |||
| 2 | Reject | Admit | Admit | 100,000 | |||
| 3 | Reject | Admit | Admit | 110,000 | |||
| 4 | Admit | Admit | Admit | Admit | 60,000 | ||
| 5 | Admit | Admit | Admit | Admit | 30,000 | ||
| 6 | Admit | 115,000 | |||||
| 7 | Admit | 75,000 | |||||
| 8 | Reject | Admit | Admit | 90,000 | |||
| 9 | Reject | Admit | Admit | 60,000 |
Regression Source: Mastering Metrics
We can see from the table that:
Some students earn high salary, in both situations
Some students earn low salary, in both situations
There are clusters of students that applied for the same universities
- How likely are they to be similar? Can we benefit from the fact they believe they are similar?
If we compare earnings from the first three individuals:
- ((110 + 100)/ 2 - 11000) = -5.000
If we compare earnings from individuals 4 and 5:
- (60 - 30) = 30.000
The average is:
- 25.000/2 = 12.500
Regression Source
Let’s create a dataframe to run regressions with the previous student’s data.
R
# Create the data frame
data <- data.frame(
id = 1:9,
earnings = c(110000, 100000, 110000, 60000, 30000, 115000, 75000, 90000, 60000),
school = c("private", "private", "public", "private", "public", "private", "private", "public", "public"),
private = c(1, 1, 0, 1, 0, 1, 1, 0, 0),
group = c(1, 1, 1, 2, 2, 3, 3, 4, 4)
)
print(data) id earnings school private group
1 1 110000 private 1 1
2 2 100000 private 1 1
3 3 110000 public 0 1
4 4 60000 private 1 2
5 5 30000 public 0 2
6 6 115000 private 1 3
7 7 75000 private 1 3
8 8 90000 public 0 4
9 9 60000 public 0 4Python
import pandas as pd
data = pd.DataFrame({
'id': range(1, 10),
'earnings': [110000, 100000, 110000, 60000, 30000, 115000, 75000, 90000, 60000],
'school': ["private", "private", "public", "private", "public", "private", "private", "public", "public"],
'private': [1, 1, 0, 1, 0, 1, 1, 0, 0],
'group': [1, 1, 1, 2, 2, 3, 3, 4, 4]
})
print(data) id earnings school private group
0 1 110000 private 1 1
1 2 100000 private 1 1
2 3 110000 public 0 1
3 4 60000 private 1 2
4 5 30000 public 0 2
5 6 115000 private 1 3
6 7 75000 private 1 3
7 8 90000 public 0 4
8 9 60000 public 0 4Stata
id earnings school private group
1. 1 110000 "private" 1 1
2. 2 100000 "private" 1 1
3. 3 110000 "public" 0 1
4. 4 60000 "private" 1 2
5. 5 30000 "public" 0 2
6. 6 115000 "private" 1 3
7. 7 75000 "private" 1 3
8. 8 90000 "public" 0 4
9. 9 60000 "public" 0 4
10. end
+-------------------------------------------+
| id earnings school private group |
|-------------------------------------------|
1. | 1 110000 private 1 1 |
2. | 2 100000 private 1 1 |
3. | 3 110000 public 0 1 |
4. | 4 60000 private 1 2 |
5. | 5 30000 public 0 2 |
|-------------------------------------------|
6. | 6 115000 private 1 3 |
7. | 7 75000 private 1 3 |
8. | 8 90000 public 0 4 |
9. | 9 60000 public 0 4 |
+-------------------------------------------+“Naive” regression all students Source
\[earnings_i = \alpha + \beta_1 Private_i + \epsilon\] What is the benefit of private education here?
Call:
lm(formula = earnings ~ private, data = data)
Residuals:
Min 1Q Median 3Q Max
-42500 -17000 8000 18000 37500
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 72500 14522 4.992 0.00158 **
private 19500 19484 1.001 0.35023
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 29040 on 7 degrees of freedom
Multiple R-squared: 0.1252, Adjusted R-squared: 0.0002116
F-statistic: 1.002 on 1 and 7 DF, p-value: 0.3502Python
OLS Regression Results
==============================================================================
Dep. Variable: earnings R-squared: 0.125
Model: OLS Adj. R-squared: 0.000
Method: Least Squares F-statistic: 1.002
Date: ter, 30 jan 2024 Prob (F-statistic): 0.350
Time: 15:38:37 Log-Likelihood: -104.13
No. Observations: 9 AIC: 212.3
Df Residuals: 7 BIC: 212.7
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 7.25e+04 1.45e+04 4.992 0.002 3.82e+04 1.07e+05
private 1.95e+04 1.95e+04 1.001 0.350 -2.66e+04 6.56e+04
==============================================================================
Omnibus: 1.011 Durbin-Watson: 2.352
Prob(Omnibus): 0.603 Jarque-Bera (JB): 0.666
Skew: -0.263 Prob(JB): 0.717
Kurtosis: 1.776 Cond. No. 2.77
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.Stata
Source | SS df MS Number of obs = 9
-------------+---------------------------------- F(1, 7) = 1.00
Model | 845000000 1 845000000 Prob > F = 0.3502
Residual | 5.9050e+09 7 843571429 R-squared = 0.1252
-------------+---------------------------------- Adj R-squared = 0.0002
Total | 6.7500e+09 8 843750000 Root MSE = 29044
------------------------------------------------------------------------------
earnings | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
private | 19500 19483.51 1.00 0.350 -26571.18 65571.18
_cons | 72500 14522.15 4.99 0.002 38160.57 106839.4
------------------------------------------------------------------------------“Naive” regression all students Source
\[earnings_i = \alpha + \beta_1 Private_i + \epsilon\] What is the benefit of private education here?
The coefficient of private is 19500, meaning that those that have private education earn 19500 more.
The problem with this design is that 1) we are including all students, even those that do not bring any “information”, and 2) we are not controlling for the differences in students’ profiles.
Let’s fix the first problem first.
What students should we not include in the model?
Students id<=5 Source
\[earnings_i = \alpha + \beta_1 Private_i + \epsilon \;,\; if\; i <=5\] What is the benefit of private education here?
Call:
lm(formula = earnings ~ private, data = subset(data, id <= 5))
Residuals:
1 2 3 4 5
20000 10000 40000 -30000 -40000
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 70000 27689 2.528 0.0856 .
private 20000 35746 0.560 0.6149
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 39160 on 3 degrees of freedom
Multiple R-squared: 0.09449, Adjusted R-squared: -0.2073
F-statistic: 0.313 on 1 and 3 DF, p-value: 0.6149Python
OLS Regression Results
==============================================================================
Dep. Variable: earnings R-squared: 0.094
Model: OLS Adj. R-squared: -0.207
Method: Least Squares F-statistic: 0.3130
Date: ter, 30 jan 2024 Prob (F-statistic): 0.615
Time: 15:38:40 Log-Likelihood: -58.694
No. Observations: 5 AIC: 121.4
Df Residuals: 3 BIC: 120.6
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 7e+04 2.77e+04 2.528 0.086 -1.81e+04 1.58e+05
private 2e+04 3.57e+04 0.560 0.615 -9.38e+04 1.34e+05
==============================================================================
Omnibus: nan Durbin-Watson: 1.304
Prob(Omnibus): nan Jarque-Bera (JB): 0.520
Skew: -0.129 Prob(JB): 0.771
Kurtosis: 1.441 Cond. No. 2.92
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.Stata
Source | SS df MS Number of obs = 5
-------------+---------------------------------- F(1, 3) = 0.31
Model | 480000000 1 480000000 Prob > F = 0.6149
Residual | 4.6000e+09 3 1.5333e+09 R-squared = 0.0945
-------------+---------------------------------- Adj R-squared = -0.2073
Total | 5.0800e+09 4 1.2700e+09 Root MSE = 39158
------------------------------------------------------------------------------
earnings | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
private | 20000 35746.02 0.56 0.615 -93759.78 133759.8
_cons | 70000 27688.75 2.53 0.086 -18117.95 158117.9
------------------------------------------------------------------------------Students id<=5 Source
\[earnings_i = \alpha + \beta_1 Private_i + \epsilon \;,\; if\; i <=5\] What is the benefit of private education here?
Students 6 and 7 only applied to Private, while students 8 and 9 did not really had a choice. So we should exclude them.
The benefit of private is now 20000.
The coefficient did not change much, but the design improved partially.
We still have an uncontrolled “heterogeneity” in the groups of students. Students 1 to 3 seem to earn more no matter their decisions.
Apples-to-Apples Source
\[earnings_i = \alpha + \beta_1 Private_i + \beta_2 Group+ \epsilon \;,\; if\; i <=5\] This is the best we can do.
R
Call:
lm(formula = earnings ~ private + dummy, data = subset(data,
id <= 5))
Residuals:
1 2 3 4 5
1.182e-11 -1.000e+04 1.000e+04 1.000e+04 -1.000e+04
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 40000 11952 3.347 0.0789 .
private 10000 13093 0.764 0.5248
dummy 60000 13093 4.583 0.0445 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 14140 on 2 degrees of freedom
Multiple R-squared: 0.9213, Adjusted R-squared: 0.8425
F-statistic: 11.7 on 2 and 2 DF, p-value: 0.07874Python
OLS Regression Results
==============================================================================
Dep. Variable: earnings R-squared: 0.921
Model: OLS Adj. R-squared: 0.843
Method: Least Squares F-statistic: 11.70
Date: ter, 30 jan 2024 Prob (F-statistic): 0.0787
Time: 15:38:43 Log-Likelihood: -52.589
No. Observations: 5 AIC: 111.2
Df Residuals: 2 BIC: 110.0
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 4e+04 1.2e+04 3.347 0.079 -1.14e+04 9.14e+04
private 1e+04 1.31e+04 0.764 0.525 -4.63e+04 6.63e+04
dummy 6e+04 1.31e+04 4.583 0.044 3665.052 1.16e+05
==============================================================================
Omnibus: nan Durbin-Watson: 2.250
Prob(Omnibus): nan Jarque-Bera (JB): 0.638
Skew: 0.000 Prob(JB): 0.727
Kurtosis: 1.250 Cond. No. 3.49
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.Stata
quiet input id earnings str7 school private group
1 110000 "private" 1 1
2 100000 "private" 1 1
3 110000 "public" 0 1
4 60000 "private" 1 2
5 30000 "public" 0 2
6 115000 "private" 1 3
7 75000 "private" 1 3
8 90000 "public" 0 4
9 60000 "public" 0 4
end
gen dummy = 1 if group == 1
replace dummy = 0 if group == 2
reg earnings private dummy if id<=5 (6 missing values generated)
(2 real changes made)
Source | SS df MS Number of obs = 5
-------------+---------------------------------- F(2, 2) = 11.70
Model | 4.6800e+09 2 2.3400e+09 Prob > F = 0.0787
Residual | 400000000 2 200000000 R-squared = 0.9213
-------------+---------------------------------- Adj R-squared = 0.8425
Total | 5.0800e+09 4 1.2700e+09 Root MSE = 14142
------------------------------------------------------------------------------
earnings | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
private | 10000 13093.07 0.76 0.525 -46334.95 66334.95
dummy | 60000 13093.07 4.58 0.044 3665.052 116334.9
_cons | 40000 11952.29 3.35 0.079 -11426.54 91426.54
------------------------------------------------------------------------------Regression
The previous regression assumes that students 1 to 3 are different that students 4 and 5.
We will find many instances like that in empirical research. E.g., industry.
The private school coefficient, in this case 10,000, implies a private-public earnings differential of this value.
Important
The Y above is used in monetary values.
Using a logged y, ln(Y) or ln(earnings), allows estimates to be interpreted as a percent change.
For instance if \(\beta=0.05\), it means that the earnings differential is 5% for those studying in private schools (conditional on the controls included in the model).
OVB again
OVB again
Regression is a way to make other things equal (ceteris paribus), but equality is generated only for variables included in the model as controls on the right-hand sided of the model.
Failure to include enough controls of the right controls still leave us with selection bias.
The regression version of the selection bias generated by the inadequate controls is called Omitted Variable Bias (OVB).
The inclusion of a control that should not be included is called “Bad Controls” problem.
OVB again
How could we calculate the OVB in this example?
\[earnings_i = 70.000 + 20.000\times Private_i \epsilon \]
\[earnings_i = 40.000 + 10.000 \times Private_i + 60.000 \times Group+ \epsilon\]
- \(\beta\) (1st regression) - \(\beta\) (second regression).
- The OVB here is 20.000 - 10.000 = 10.000.
- Meaning that the \(\beta\) (1st regression) is 10.000 higher than what it should be.
OVB again
How could we calculate the OVB in this example?
We could calculate the bias by estimating:
\[Private=\alpha + \beta_{omitted} \times Group + \epsilon\]
Then,
\[\beta_{omitted} \times \beta_{missing} = 0.1667 * 60.000 = 10.000\]
The OVB is 10.000, meaning that the first model (the one with the omitted variable) estimates a Beta that is 10.000 higher than it should be.
OVB again
Call:
lm(formula = private ~ dummy, data = subset(data, id <= 5))
Residuals:
1 2 3 4 5
0.3333 0.3333 -0.6667 0.5000 -0.5000
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.5000 0.4410 1.134 0.339
dummy 0.1667 0.5693 0.293 0.789
Residual standard error: 0.6236 on 3 degrees of freedom
Multiple R-squared: 0.02778, Adjusted R-squared: -0.2963
F-statistic: 0.08571 on 1 and 3 DF, p-value: 0.7888[1] 10002Python
OLS Regression Results
==============================================================================
Dep. Variable: private R-squared: 0.028
Model: OLS Adj. R-squared: -0.296
Method: Least Squares F-statistic: 0.08571
Date: ter, 30 jan 2024 Prob (F-statistic): 0.789
Time: 15:38:47 Log-Likelihood: -3.4565
No. Observations: 5 AIC: 10.91
Df Residuals: 3 BIC: 10.13
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 0.5000 0.441 1.134 0.339 -0.903 1.903
dummy 0.1667 0.569 0.293 0.789 -1.645 1.978
==============================================================================
Omnibus: nan Durbin-Watson: 2.881
Prob(Omnibus): nan Jarque-Bera (JB): 0.749
Skew: -0.394 Prob(JB): 0.688
Kurtosis: 1.276 Cond. No. 2.92
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.10002.0Stata
quiet input id earnings str7 school private group
1 110000 "private" 1 1
2 100000 "private" 1 1
3 110000 "public" 0 1
4 60000 "private" 1 2
5 30000 "public" 0 2
6 115000 "private" 1 3
7 75000 "private" 1 3
8 90000 "public" 0 4
9 60000 "public" 0 4
end
gen dummy = 1 if group == 1
replace dummy = 0 if group == 2
reg private dummy if id<=5
di .1666667 * 60000 (6 missing values generated)
(2 real changes made)
Source | SS df MS Number of obs = 5
-------------+---------------------------------- F(1, 3) = 0.09
Model | .033333333 1 .033333333 Prob > F = 0.7888
Residual | 1.16666667 3 .388888889 R-squared = 0.0278
-------------+---------------------------------- Adj R-squared = -0.2963
Total | 1.2 4 .3 Root MSE = .62361
------------------------------------------------------------------------------
private | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
dummy | .1666667 .569275 0.29 0.789 -1.645021 1.978354
_cons | .5 .4409586 1.13 0.339 -.9033269 1.903327
------------------------------------------------------------------------------
10000.002OVB again
So what?
Anticipating the effect of the omitted variable on the non-omitted variable can tell you the sign of the bias.
Then you can know if the bias is attenuating or increasing the effect you are investigating.
If attenuating, the problem is smaller than if it is increasing
OVB again
Regressions
The previous examples show that we can run regressions and find correlations …
… And we can run regressions and find causal effects.
But we need to control for all relevant variables, otherwise we have the OVB problem.
Should you not look careful to your data, you’d miss the inclusion of the variable
group.The results show that you may estimate a spurious coefficient twice the size of the “true” coefficient.
Bad Controls Problem
Bad Controls Problem
Bad controls are variables that are also outcome of the treatment being studied.
A Bad control could very well be a dependent variable of the treatment as well.
Good controls are variables that you can think as being fixed at the time of the treatment.
Let’s return to the model.
\[earnings_i = \alpha + \beta_1 Private_i + \beta_2 Group+ \epsilon \;,\; if\; i <=5\]
Assuming you also have the occupation of the students at the time of earnings. Should you include occupation in the model?
\[earnings_i = \alpha + \beta_1 Private_i + \beta_2 Group + \beta_3 Occupation + \epsilon \;,\; if\; i <=5\]
Reasoning: “We should use occupation as control because it would be wise to look at the effect of education on earnings only for those within an occupation”.
What is the problem with this reasoning?
Bad Controls Problem
The problem is that studying in private would increase the chances of getting a white-collar occupation, i.e., private education (treatment) affects the occupation (bad control).
In this case, should you include occupation as control, the coefficient of interest no longer has a causal interpretation.
This is a very common problem in empirical research.
It is not hard to come up with stories of why a control is a bad control.
Randomization
Randomization
Now I want to discuss the idea of randomization
Suppose you have developed a treatment (e.g., a program) that you believe will increase the ‘motivation’ of employees of a factory.
You have 100 employees to use in an experiment to test your claim that the treatment will increase motivation.
- You randomly allocate 50 employees to receive the treatment. The other 50 are part of the control group.
- You treat all employees in the same manner, except for the treatment.
Using the data available, this is the difference in motivation between the treatment and control groups (next slide):
Randomization
R
library(readxl)
library(ggplot2)
library(tidyverse)
library(dplyr)
data <- read_excel("files/part_3_data.xlsx", range = "A1:C101")
# Box plot control vs treatment groups
ggplot(data, aes(y=motivation, fill=group)) +
geom_boxplot()+
theme(plot.title = element_text(color="black", size=30, face="bold"),
panel.background = element_rect(fill = "grey95", colour = "grey95"),
axis.text.y = element_text(face="bold", color="black", size = 18),
axis.text.x = element_blank(),
legend.title = element_blank(),
legend.key.size = unit(3, "cm"))
Python
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# Read data from Excel file
data = pd.read_excel("files/part_3_data.xlsx")
# Create a box plot of control vs treatment groups using seaborn
plt.figure(figsize=(7, 5))
sns.set(style='whitegrid')
sns.boxplot(x='group', y='motivation', data=data, palette='Set2')
plt.title("Box Plot of Control vs Treatment Groups", fontsize=18)
plt.xlabel("Group", fontsize=14)
plt.ylabel("Motivation", fontsize=14)
plt.show()
Randomization
The calculated means are below. And they are statistically different.
R
$Control
Min. 1st Qu. Median Mean 3rd Qu. Max.
16.70 19.70 20.70 20.80 22.27 24.60
$Treatment
Min. 1st Qu. Median Mean 3rd Qu. Max.
17.60 20.52 22.50 22.27 23.77 26.50
Welch Two Sample t-test
data: motivation by group
t = -3.7301, df = 94.879, p-value = 0.0003258
alternative hypothesis: true difference in means between group Control and group Treatment is not equal to 0
95 percent confidence interval:
-2.2493176 -0.6866824
sample estimates:
mean in group Control mean in group Treatment
20.800 22.268 Stata
(3 vars, 100 obs)
-------------------------------------------------------------------------------
-> group = Control
Variable | Obs Mean Std. dev. Min Max
-------------+---------------------------------------------------------
motivation | 50 20.8 1.780392 16.7 24.6
-------------------------------------------------------------------------------
-> group = Treatment
Variable | Obs Mean Std. dev. Min Max
-------------+---------------------------------------------------------
motivation | 50 22.268 2.1388 17.6 26.5
| e(b) e(count) e(se) e(t) e(df_t)
-------------+-------------------------------------------------------
motivation | -1.468 100 .3935546 -3.730105 98
| e(p_l) e(p) e(p_u) e(N_1) e(mu_1)
-------------+-------------------------------------------------------
motivation | .0001604 .0003208 .9998396 50 20.8
| e(N_2) e(mu_2)
-------------+----------------------
motivation | 50 22.268 Randomization
Is there evidence that the program has increased motivation?
well, if you randomly split a group of 100 people into two groups of 50, you certainly wouldn’t get the same mean motivation in both groups even if you treated them exactly alike.
Maybe the difference that we see is just such a difference?
How can we test this hypothesis?
Randomization
Solution:
Suppose the treatment had no effect, and the employees developed their motivation independently of the treatment.
What is the chance that the 50 employees randomly assigned to the treatment group would have an average at least 1.47 (22.27 - 20.80) points higher than the average motivation of the employees randomly assigned to the control group?
Randomization
Steps
Randomly split the 100 employees that we observed in this experiment into two groups of 50.
Note the difference in the mean motivation between the two groups.
Repeat 1 and 2 a total of 10,000 times.
Note the proportion of times the difference is at least 1.47 (22.27 - 20.80).
Randomization
R
# Load necessary libraries
data <- read_excel("files/part_3_data.xlsx", range = "A1:C101")
comb <- 10000
df <- data.frame(matrix(ncol = 2, nrow = comb))
colnames(df) <- c("order" ,"diff")
# Create the loop for randomization:
for (i in seq(from = 1, to = comb)) {
set.seed(i)
data$temp <- runif(100, min = 0, max = 1) # Creating 100 random numbers 0 to 1
data <- data[order(data$temp),] # Sorting data by the random numbers generated in the previous row
data$rank <- rank(data$temp) # Ranking by the random numbers
# The row below defines the treatment group based on the random numbers generated. This is where we guarantee randomization
data$status_rank <- case_when(data$rank <= 50 ~ "Control_rand", data$rank > 50 ~ "Treated_rand")
# Calculate the new means of the new groups. Need to transpose data.
means <- t(as.data.frame(tapply(data$motivation, data$status_rank, mean)))
# Moving the new means to df. Each row is the difference of means
df[i, 1] <- i
df[i, 2] <- means[1, 2] - means[1, 1]
rm(means) # Deleting value
data = subset(data, select = -c(temp, rank, status_rank)) # Deleting variables
}
# Calculate a suitable binwidth for the histogram
binwidth <- (max(df$diff) - min(df$diff)) / sqrt(length(df$diff))
# Create a histogram of the differences with the calculated binwidth
ggplot(df, aes(x = diff)) +
geom_histogram(binwidth = binwidth, fill = "blue", color = "black") +
labs(title = "Distribution of Differences", x = "Difference", y = "Frequency")
Stata
import excel "files/part_3_data.xlsx", cellrange(A1:C101) firstrow clear
set seed 472195
sort group
set obs 10000
egen fin_order = seq()
sort fin_order
summarize
gen av_diff=.
local i = 1
while `i'<=10000 {
sort fin_order
gen rand_num`i' = uniform() if !missing(motivation)
egen ordering`i' = rank(rand_num`i')
sort ordering`i'
gen group`i' = ""
replace group`i' = "T" if ordering <= 50
replace group`i' = "C" if ordering > 50 & ordering<=100
qui summ motivation if group`i'=="T"
scalar avT = `r(mean)'
qui summ motivation if group`i'=="C"
scalar avC = `r(mean)'
sort fin_order
replace av_diff = avT-avC in `i'
drop rand_num`i' ordering`i' group`i'
local i = `i' + 1
}
histogram av_diff, frequency kdensity
graph export "files/graph3_6.png" , replace
Randomization
The mean difference was as far from 0 as 1.5 for only a few out of the 10,000 random divisions of the data into two groups of 50.
Thus, the difference between the mean motivation would almost always be less than the observed difference of 1.47 (22.27 - 20.80) if the treatment had no effect.
It seems reasonable to believe that the treatment caused the difference in motivation.
Measurement Error problem
Measurement Error problem
The measurement error problem has a similar statistical structure to the omitted variable bias (OVB).
“Classical” random measurement error for the \(y\) will inflate standard errors but will not lead to biased coefficients.
- \(y^{*} = y + \sigma_{1}\)
- If you estimante \(y^{*} = f(x)\), you have \(y + \sigma_{1} = x + \epsilon\)
- \(y = x + u\)
- where \(u = \epsilon - \sigma_{1}\)
Measurement Error problem
“Classical” random measurement error in x’s will bias coefficient estimates toward zero.
\(x^*=x+\sigma_2\)
Imagine that \(x^*\) is a bunch of noise. It would not explain anything. Thus, your results are biased toward zero.
Measurement Error problem
A example using one of the Wooldridge’s datasets.
R
library(foreign)
library(jtools)
data <- read.dta("files/CEOSAL1.dta")
set.seed(2)
data$salary_noise <- data$salary + runif(length((data$salary)), min=-100, max= 100)
data$roe_noise <- data$roe + runif(length((data$roe)), min=-100, max= 100)
# OLS model
model1 <- lm(data$salary ~ data$roe)
model2 <- lm(data$salary ~ data$roe_noise)
model3 <- lm(data$salary_noise ~ data$roe)
#summary(model1)
#summary(model2)
#summary(model3)
export_summs(model1, model2, model3, digits = 3 , model.names = c("Roe", "Roe (X) with noise", "Salary (y) with noise") )| Roe | Roe (X) with noise | Salary (y) with noise | |
| (Intercept) | 963.191 *** | 1269.739 *** | 964.058 *** |
| (213.240) | (97.356) | (214.588) | |
| data$roe | 18.501 | 18.318 | |
| (11.123) | (11.194) | ||
| data$roe_noise | 0.868 | ||
| (1.593) | |||
| N | 209 | 209 | 209 |
| R2 | 0.013 | 0.001 | 0.013 |
| *** p < 0.001; ** p < 0.01; * p < 0.05. | |||
Python
import pandas as pd
import numpy as np
import statsmodels.api as sm
import statsmodels.formula.api as smf
from statsmodels.iolib.summary2 import summary_col
data = pd.read_stata("files/CEOSAL1.dta")
np.random.seed(2)
# Add noise to the 'salary' and 'roe' columns
data['salary_noise'] = data['salary'] + np.random.uniform(-100, 100, len(data))
data['roe_noise'] = data['roe'] + np.random.uniform(-100, 100, len(data))
# OLS model
model1 = smf.ols(formula='salary ~ roe', data=data).fit()
model2 = smf.ols(formula='salary ~ roe_noise', data=data).fit()
model3 = smf.ols(formula='salary_noise ~ roe', data=data).fit()
# Create a summary table for all regressions
results = summary_col([model1, model2, model3],
model_names=['Reg 1', 'Reg 2', 'Reg 3'],
stars=True,
float_format='%0.2f')
# Print the summary table
print(results)
=============================================
Reg 1 Reg 2 Reg 3
---------------------------------------------
Intercept 963.19*** 1262.12*** 966.97***
(213.24) (98.19) (213.37)
R-squared 0.01 0.00 0.01
R-squared Adj. 0.01 -0.00 0.01
roe 18.50* 17.92
(11.12) (11.13)
roe_noise 1.25
(1.63)
=============================================
Standard errors in parentheses.
* p<.1, ** p<.05, ***p<.01Stata
(est1 stored)
(est2 stored)
(est3 stored)
------------------------------------------------------------
(1) (2) (3)
salary salary salary_noise
------------------------------------------------------------
roe 18.50 18.14
(1.66) (1.63)
roe_noise 0.0336
(0.02)
_cons 963.2*** 1280.4*** 966.1***
(4.52) (12.71) (4.53)
------------------------------------------------------------
N 209 209 209
------------------------------------------------------------
t statistics in parentheses
* p<0.05, ** p<0.01, *** p<0.001More about Regressions
Regression
Linear regressions are the workhorse tool in econometrics
- Simplicity: straightforward to understand, implement, and visualize.
- Interpretability: coefficients have clear interpretations.
- represents the change in the Y for a one-unit change in the X, holding all other variables constant.
- Versatility: simple linear regression or multiple linear regression.
- Assumptions: linearity, independence of errors, homoscedasticity, and normality of errors.
- Baseline Model: You can compare the performance of more advanced models to linear regression.
- Estimation: provides clear estimates of the coefficients’ confidence intervals and hypothesis testing.
Regression
In this setting, the variables \(y\) and \(x\) can have several names.
| Y | X |
|---|---|
| Dependent variable | Independent variable |
| Explained variable | Explanatory variable |
| Response variable | Control variable |
| Predicted variable | Predictor variable |
| Regressand | Regressor |
Regression
Broadly, we are interested in how y is explained by x?
- \(y_i = \alpha + \beta_1 x_i + \epsilon\)
Perhaps \(\epsilon\) is the most important part of a regression.
The interpretation is “everything that is not explained by X and that explains Y”.
A comment
Usually, the literature uses \(\epsilon\) for the “estimated” residual.
And \(\mu\) for the “true” residual, which necessarily implies that the assumptions hold.
At the end od the day, you don’t need to worry to much with the notation of this term because we are always in the “estimated world”, and almost never in the “true world”.
The “true world” implies that you are studying the population or that you have a true random sample of the population
- \(y_i = \alpha + \beta_1 x_i + \mu\)
Regression
Remember
- \(y, x\), and \(\mu\) are random variables
- \(y and x\) are observable
- \(\mu\) and \(\beta\) are unobservable
- \(\mu\) captures everything that determines y after accounting for x
Our goal is to estimate β
Regression
There are some assumptions/requirements about \(\mu\) in a OLS
First assumption
E(\(\mu\)) = 0
- This is a simple assumption, not strong at all.
- It simply assumes that the average of \(\mu\) is zero in the population.
- Basically, any non-zero mean is absorbed by the intercept
- Say that E(\(\mu\)) = k
- We could rewrite \(\mu = k + w\), where E(w)=0
- Then, model becomes \(y=(\alpha +𝑘) + \beta𝑥+𝑤\)
- Intercept is now just (α + k), and error, w, is mean zero
Regression
Second assumption
- E(\(\mu\)|x) = E(\(\mu\)) for all values of x
- It says that the average value of \(\mu\) does not depend on the value of x (i.e., the slice of the population you are looking at).
- We say that \(\mu\) is mean-independent of x.
- This is true if the X and the \(\mu\) are independent to each other.
- Implies that x and \(\mu\) are uncorrelated.
- Conditional Mean Independence (CMI).
- This is one of the keys assumption to causal inference.
Regression
Second assumption
Example
Let’s say the model is:
\[wage = \alpha + \beta Schooling_{years} + \epsilon\]
- where \(\epsilon\) represents unobserved ability.
Does CMI hold?
That is E(ability|x=8)=E(ability|x=10)=E(ability|x=12)?
Probably not, because the unobserved ability should depend on the years of schooling.
The solution (not trivial) would be to include ability as a new X.
Regression
Another example
Consider the following model (with only one X)
\[Leverage_i = \alpha + \beta_1 Profitability_i + \mu_i\]
CMI says that, to every firm i, \(\mu\) is the same, even when firms have different profitability.
Can you think on examples when this assumption may not hold in this model?
unprofitable firms have higher bankruptcy risk, which should make them to have lower leverage (tradeoff theory).
unprofitable firms have low cash, which should make them to have more leverage (pecking order theory).
Regression
The discussion of whether the CMI holds is the origin of the “endogeneity” problem.
You will face reviewers arguing reasons of why the CMI might not hold in your case.
Many will criticize a model by saying it has an “endogeneity problem”, whithout explaining more.
- This is very generic. Don’t do that!
They should explain what is the source of the problem that is making the model violate CMI.
- OVB, selection bias, reverse causality, simultaneity, etc?
Generally speaking, endogeneity refers to a violation of CMI, meaning that \(x\) and \(\mu\) are correlated.
This is always a plausible possibility, since \(\mu\) carries a lot of stuff (something must be correlated with X).
Regression
Third assumption
Combining 1 and 2 leads to
- E(\(\mu\)|x) = 0
- This is a very important assumption called zero conditional mean assumption.
Ordinary Least Squares
Our focus is to find estimates for \(\alpha\) and \(\beta\). Should we have access to the population, it would be easy. We could write:
\[y_i= \alpha + \beta_1x_i + \mu\]
But remember that,
\[E(u) = 0\] \[E(u|x) = 0\]
The second bullet implies that the correlation between x and \(\mu\) is zero (we can write that as E(x,u) = 0).
Important
Remember: \(\alpha\) and \(\beta\) are parameters to be estimated (i.e., constants), while \(X\) and \(Y\) are variables
Regression
So we can write that (in the population)
\(E(y - \alpha - \beta_1x ) = 0\)
\((x[y - \alpha - \beta_1x ]) = 0\)
So we can write that (in the sample)
\(\frac{1}{n} \sum_{i=1}^n (y_i - \hat{\alpha} - \hat{\beta_1} x_i ) = 0\) , We will use this to find \(\alpha\):
\(\frac{1}{n} \sum_{i=1}^n (x_i [y_i - \hat{\alpha} - \hat{\beta_1} x_i ]) = 0\) , We will use this to find \(\beta\):
Finding \(\alpha\)
From before:
\[\frac{1}{n} \sum_{i=1}^n (y_i - \hat{\alpha} - \hat{\beta_1} x_i ) =0\]
Passing the sum operator through
\[\frac{1}{n}\sum_{i=1}^n(y_i) - \frac{1}{n}\sum_{i=1}^n(\hat{\alpha}) - \frac{1}{n} \sum_{i=1}^n(\hat{\beta_1} x_i )=0\]
Coefficients are constants, so we can get rid of the sum operator.
\[\frac{1}{n}\sum_{i=1}^n(y_i) - \hat{\alpha} - \hat{\beta_1} \frac{1}{n} \sum_{i=1}^n(\ x_i )=0\]
Finding \(\alpha\)
- We know that \(\frac{1}{n}\sum_{i=1}^n(y_i)\) is \(\bar{y_i}\) (the mean)
\[\bar{y_i} - \hat{\alpha} - \hat{\beta_1} \bar{x_i}=0\]
So we write:
\[\hat{\alpha} = \bar{y_i} - \hat{\beta_1} \bar{x_i}\]
Easy Peasy 😀
Finding \(\beta\)
From before:
\[\frac{1}{n} \sum_{i=1}^n (x_i [y_i - \hat{\alpha} - \hat{\beta_1} x_i ]) = 0\]
But now we have:
\[\hat{\alpha} = \bar{y_i} - \hat{\beta_1} \bar{x_i}\]
Thus,
\[\frac{1}{n} \sum_{i=1}^n (x_i [y_i - (\bar{y_i} - \hat{\beta_1} \bar{x_i}) - \hat{\beta_1} x_i ]) = 0\]
Finding \(\beta\)
Turning into
\[\frac{1}{n} \sum_{i=1}^n (x_i [y_i - \bar{y_i} ]) - \frac{1}{n} \sum_{i=1}^n (x_i [\hat{\beta_1} x_i - \hat{\beta_1} \bar{x_i} ]) = 0\]
Or
\[\frac{1}{n} \sum_{i=1}^n (x_i [y_i - \bar{y_i} ]) = \hat{\beta_1} \frac{1}{n} \sum_{i=1}^n (x_i [ x_i - \bar{x_i} ]) \]
Last step (I am skipping some steps here)
\[\frac{1}{n} \sum_{i=1}^n (x_i - \bar{x} )(y_i - \bar{y_i} ) = \hat{\beta_1} \frac{1}{n} \sum_{i=1}^n (x_i - \bar{x_i} )^2 \]
Finding \(\beta\)
If the variance of x is not zero, we can write \(\beta\) as
\[\hat{\beta_1} = \frac{\sum_i^n (x_i - \bar{x})(y_i - \bar{y})}{\sum_i^n (x_i - \bar{x})^2} = \frac{Covariance(x_i,y_i)}{Variance(x_i)}\]
Finding \(\mu\)
Now that we have \(\hat{Y_i}=\hat{\alpha} + \hat{\beta_1} X_i\), we can estimate the residual \(\mu\)
\[\hat{\mu} = Y_i - \hat{Y_i}\]
Which is the same as:
\[\hat{\mu} = Y_i - \hat{\alpha} - \hat{\beta_1}x_i\]
Most residuals will not be 0, meaning they do not lie on the best fitting line.
Finding \(\mu\)
The job of an OLS model is find the parameters to minimize the squared error (i.e., to find the best fitting line).
\[\sum_{i=1}^n \hat{\mu}^2 = \sum_{i=1}^n(Y_i - \hat{Y_i})^2\]
Regression (Source)
Another example of regression. The differences in the coefficients are due to the differences in the seed of the random variables generator.
R
Call:
lm(formula = y ~ x, data = tb)
Residuals:
Min 1Q Median 3Q Max
-51.528 -8.152 -0.173 7.978 44.718
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.04991 0.11890 -0.42 0.675
x 5.55690 0.11745 47.31 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 11.89 on 9998 degrees of freedom
Multiple R-squared: 0.1829, Adjusted R-squared: 0.1828
F-statistic: 2238 on 1 and 9998 DF, p-value: < 2.2e-16Python
import pandas as pd
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
np.random.seed(1)
obs = 10000
data = pd.DataFrame({
'x': np.random.normal(size=obs),
'u': np.random.normal(size=obs),
})
data['y'] = 5.5 * data['x'] + 12 * data['u']
X = sm.add_constant(data['x'])
model = sm.OLS(data['y'], X).fit()
print(model.summary()) OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.183
Model: OLS Adj. R-squared: 0.183
Method: Least Squares F-statistic: 2237.
Date: ter, 30 jan 2024 Prob (F-statistic): 0.00
Time: 15:40:47 Log-Likelihood: -39049.
No. Observations: 10000 AIC: 7.810e+04
Df Residuals: 9998 BIC: 7.812e+04
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 0.1114 0.120 0.927 0.354 -0.124 0.347
x 5.6887 0.120 47.293 0.000 5.453 5.924
==============================================================================
Omnibus: 0.640 Durbin-Watson: 2.050
Prob(Omnibus): 0.726 Jarque-Bera (JB): 0.672
Skew: -0.012 Prob(JB): 0.715
Kurtosis: 2.968 Cond. No. 1.01
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.Number of observations (_N) was 0, now 10,000.
Source | SS df MS Number of obs = 10,000
-------------+---------------------------------- F(1, 9998) = 2206.80
Model | 327141.413 1 327141.413 Prob > F = 0.0000
Residual | 1482125.8 9,998 148.242229 R-squared = 0.1808
-------------+---------------------------------- Adj R-squared = 0.1807
Total | 1809267.22 9,999 180.944816 Root MSE = 12.175
------------------------------------------------------------------------------
y | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
x | 5.598296 .119172 46.98 0.000 5.364695 5.831897
_cons | -.0750109 .1217548 -0.62 0.538 -.3136748 .163653
------------------------------------------------------------------------------Regression (Source)
Another example of regression. The differences in the coefficients are due to the differences in the seed of the random variables generator.
R
library(tidyverse)
set.seed(1)
tb <- tibble(
x = rnorm(10000),
u = rnorm(10000),
y = 5.5*x + 12*u # notice that I am defining the beta1 here. The 5.5 is the "true" beta we want to estimate.
)
reg_tb <- lm(y ~ x, data=tb)
tb %>%
lm(y ~ x, .) %>%
ggplot(aes(x=x, y=y)) +
ggtitle("OLS Regression Line") +
geom_point(size = 0.05, color = "black", alpha = 0.5) +
geom_smooth(method = lm, color = "black") +
annotate("text", x = -1.5, y = 30, color = "red",
label = paste("Intercept = ", reg_tb$coefficients[1])) +
annotate("text", x = 1.5, y = -30, color = "blue",
label = paste("Slope =", reg_tb$coefficients[2]))
Python
import pandas as pd
import numpy as np
import statsmodels.api as sm
import seaborn as sns
import matplotlib.pyplot as plt
# Create a scatterplot with the OLS regression line using Seaborn
sns.set(style='whitegrid')
plt.figure(figsize=(7, 5))
sns.scatterplot(x='x', y='y', data=data, color='black', alpha=0.5, s=5)
sns.regplot(x='x', y='y', data=data, color='black', scatter=False, line_kws={'color':'black'})
plt.title('OLS Regression Line')
plt.annotate(f'Intercept = {model.params[0]:.2f}', xy=(-1.5, 30), color='red')
plt.annotate(f'Slope = {model.params[1]:.2f}', xy=(1.5, -30), color='blue')
plt.show()
Stata
set seed 1
set obs 10000
gen x = rnormal()
gen u = rnormal()
gen y = 5.5*x + 12*u
reg y x
predict yhat1
gen yhat2 = -0.0750109 + 5.598296*x
predict uhat1, residual
gen uhat2=y-yhat2
qui sum uhat*
twoway (lfit y x, lcolor(black) lwidth(medium)) (scatter y x, mcolor(black) msize(tiny) msymbol(point)), title(OLS Regression Line)
qui graph export "files/graph3.svg", replace
Regression (Source)
Using the previous regressions, we can show that:
\(\hat{y_i} = \hat{\alpha} + \hat{\beta_1} x_i\)
\(\hat{\mu_i} = y_i - \hat{y_i}\)
R
library(tidyverse)
set.seed(1)
tb <- tibble(
x = rnorm(10000),
u = rnorm(10000),
y = 5.5*x + 12*u # notice that I am defining the beta1 here. The 5.5 is the "true" beta we want to estimate.
)
reg_tb <- lm(y ~ x, data=tb)
tb <- tb %>%
mutate(
yhat1 = predict(lm(y ~ x, .)),
yhat2 = reg_tb$coefficients[1] + reg_tb$coefficients[2]*x,
uhat1 = residuals(lm(y ~ x, .)),
uhat2 = y - yhat2
)
summary(tb[-1:-3]) yhat1 yhat2 uhat1 uhat2
Min. :-20.45096 Min. :-20.45096 Min. :-51.5275 Min. :-51.5275
1st Qu.: -3.79189 1st Qu.: -3.79189 1st Qu.: -8.1520 1st Qu.: -8.1520
Median : -0.13842 Median : -0.13842 Median : -0.1727 Median : -0.1727
Mean : -0.08624 Mean : -0.08624 Mean : 0.0000 Mean : 0.0000
3rd Qu.: 3.71578 3rd Qu.: 3.71578 3rd Qu.: 7.9778 3rd Qu.: 7.9778
Max. : 21.12342 Max. : 21.12342 Max. : 44.7176 Max. : 44.7176 Python
import pandas as pd
import numpy as np
import statsmodels.api as sm
np.random.seed(1)
obs = 10000
x = np.random.normal(size=obs)
u = np.random.normal(size=obs)
y = 5.5 * x + 12 * u
X = sm.add_constant(x)
model = sm.OLS(y, X).fit()
tb = pd.DataFrame({'x': x, 'u': u, 'y': y})
tb['yhat1'] = model.predict(X)
tb['uhat1'] = y - tb['yhat1']
tb['yhat2'] = model.params[0] + model.params[1] * x
tb['uhat2'] = y - tb['yhat2']
print(tb[['yhat1','yhat2', 'uhat1','uhat2']].describe()) yhat1 yhat2 uhat1 uhat2
count 10000.000000 10000.000000 1.000000e+04 1.000000e+04
mean 0.166975 0.166975 -1.691092e-16 -1.691092e-16
std 5.682040 5.682040 1.201339e+01 1.201339e+01
min -20.688875 -20.688875 -4.142425e+01 -4.142425e+01
25% -3.659775 -3.659775 -8.199882e+00 -8.199882e+00
50% 0.159473 0.159473 4.497835e-02 4.497835e-02
75% 3.933075 3.933075 8.147307e+00 8.147307e+00
max 23.018769 23.018769 5.000751e+01 5.000751e+01Stata
(option xb assumed; fitted values)
Variable | Obs Mean Std. dev. Min Max
-------------+---------------------------------------------------------
yhat1 | 10,000 -.0797351 5.719914 -23.06927 22.47639
yhat2 | 10,000 -.0797351 5.719913 -23.06927 22.47639
uhat1 | 10,000 -3.53e-09 12.17487 -49.8996 42.15174
uhat2 | 10,000 -1.72e-08 12.17487 -49.8996 42.15174Properties of OLS
Properties of OLS
We can easily show that (remember from before)
\[\sum_i^n(y_i - \hat{\alpha} - \hat{\beta_1} x_i) = 0\]
And that
\[\sum_i^n \hat{\mu} = 0\]
The graphs next slide shows a spherical figure, suggesting that the residual is not correlated with the the fitted values (\(\hat{y_i}\))
Properties of OLS
R
library(tidyverse)
set.seed(1)
tb <- tibble(
x = rnorm(10000),
u = rnorm(10000),
y = 5.5*x + 12*u # notice that I am defining the beta1 here. The 5.5 is the "true" beta we want to estimate.
)
reg_tb <- lm(y ~ x, data=tb)
tb <- tb %>%
mutate(
yhat1 = predict(lm(y ~ x, .)),
yhat2 = reg_tb$coefficients[1] + reg_tb$coefficients[2]*x,
uhat1 = residuals(lm(y ~ x, .)),
uhat2 = y - yhat2
)
tb %>%
lm(uhat1 ~ yhat1 , .) %>%
ggplot(aes(x=yhat1, y=uhat1)) +
geom_point(size = 0.1, color = "black") +
geom_smooth(method = lm, color = "black")
Python
import pandas as pd
import numpy as np
import statsmodels.api as sm
np.random.seed(1)
obs = 10000
x = np.random.normal(size=obs)
u = np.random.normal(size=obs)
y = 5.5 * x + 12 * u
X = sm.add_constant(x)
model = sm.OLS(y, X).fit()
tb = pd.DataFrame({'x': x, 'u': u, 'y': y})
tb['yhat1'] = model.predict(X)
tb['uhat1'] = y - tb['yhat1']
tb['yhat2'] = model.params[0] + model.params[1] * x
tb['uhat2'] = y - tb['yhat2']
model = sm.OLS(tb['uhat1'], sm.add_constant(tb['yhat1'])).fit()
# Create a scatter plot with a regression line
sns.set(style="whitegrid")
plt.figure(figsize=(7, 4.5))
sns.scatterplot(x='yhat1', y='uhat1', data=tb, size=0.05, color='black', alpha=0.5)
sns.regplot(x='yhat1', y='uhat1', data=tb, scatter=False, color='black')
plt.xlabel('yhat1')
plt.ylabel('uhat1')
plt.title('Scatter Plot of uhat1 vs. yhat1')
plt.show()
Properties of OLS
Similarly, we can easily show that
\[\sum_i^nx_i(y_i - \hat{\alpha} - \hat{\beta_1} x_i) = 0\]
And that
\[\sum_i^nx_i\hat{\mu} = 0\]
Meaning that the sample covariance between the X and the residual will be always zero.
Properties of OLS
R
library(tidyverse)
set.seed(1)
tb <- tibble(
x = rnorm(10000),
u = rnorm(10000),
y = 5.5*x + 12*u # notice that I am defining the beta1 here. The 5.5 is the "true" beta we want to estimate.
)
reg_tb <- lm(y ~ x, data=tb)
tb <- tb %>%
mutate(
yhat1 = predict(lm(y ~ x, .)),
yhat2 = reg_tb$coefficients[1] + reg_tb$coefficients[2]*x,
uhat1 = residuals(lm(y ~ x, .)),
uhat2 = y - yhat2
)
tb %>%
lm(uhat1 ~ x , .) %>%
ggplot(aes(x=x, y=uhat1)) +
geom_point(size = 0.1, color = "black") +
geom_smooth(method = lm, color = "black")
Python
import pandas as pd
import numpy as np
import statsmodels.api as sm
np.random.seed(1)
obs = 10000
x = np.random.normal(size=obs)
u = np.random.normal(size=obs)
y = 5.5 * x + 12 * u
X = sm.add_constant(x)
model = sm.OLS(y, X).fit()
tb = pd.DataFrame({'x': x, 'u': u, 'y': y})
tb['yhat1'] = model.predict(X)
tb['uhat1'] = y - tb['yhat1']
tb['yhat2'] = model.params[0] + model.params[1] * x
tb['uhat2'] = y - tb['yhat2']
model = sm.OLS(tb['uhat1'], sm.add_constant(tb['yhat1'])).fit()
# Create a scatter plot with a regression line
sns.set(style="whitegrid")
plt.figure(figsize=(7, 4.5))
sns.scatterplot(x='x', y='uhat1', data=tb, size=0.05, color='black', alpha=0.5)
sns.regplot(x='x', y='uhat1', data=tb, scatter=False, color='black')
plt.xlabel('x')
plt.ylabel('uhat1')
plt.title('Scatter Plot of uhat1 vs. x')
plt.show()
Properties of OLS
Let’s say you estimate a model and find the \(\hat{\mu}\).
If you calculate the correlation between the X and \(\hat{\mu}\), you will find zero.
This is by construction! It is not an evidence that CMI is nos violated.
In fact, the OLS “assumes” and “forces” zero correlation.
It is intuitive: if you are “forcing” zero correlation when the correlation is not in fact zero, your coefficients will be biased.
The previous graphs actually show zero correlation. But that is expected and does not suggest the model is not violating CMI.
At the end of the day, CMI is untestable and unverifiable.
Goodness-of-fit
Goodness-of-fit
Understanding what SSR, SSE and SST mean
- SSE = Sum of Squares Explained = \(\sum_i^n(\hat{y_i}-\bar{y})^2\)
- SSR = Sum of Squares Residuals = \(\sum_i^n\hat{\mu}^2\)
- SST = Sum of Squares Total = SSE + SSR = \(\sum_i^n(y_i-\hat{y_i})^2\)
R-squared is simply the ratio of portion explained over the total that could be explained.
\[R^2 = \frac{SSE}{SST} = 1-\frac{SSR}{SST}\]
Goodness-of-fit
Goodness-of-fit
You can think this way:
- If X does not explain Y, then the best predictor of Y is \(\bar{y}\). In that case, your model does not explain anything of Y, thus \(R^2\) is zero, and \(\hat{y_i}=\bar{y}\)
- If X partially explains Y, then \(\hat{y_i} \neq \bar{y}\), meaning that \(\hat{y_i}\) has some inclination (like the figure next slide). This means that \(SSE>0\) and your \(R^2>0\) but \(R^2<1\)
- Whatever is not explained by \(\hat{y_i}\) is left to \(\sum_i^2\hat{\mu}^2\), meaning that SSR will be non-zero.
- The ratio of the portion that you can explain by \(\hat{y_i}\) over the total that is to be explained \(y_i-\hat{y_i}\) if the \(R^2\).
Goodness-of-fit
R
[1] 1281.12R
Call:
lm(formula = salary ~ roe)
Residuals:
Min 1Q Median 3Q Max
-1160.2 -526.0 -254.0 138.8 13499.9
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 963.19 213.24 4.517 1.05e-05 ***
roe 18.50 11.12 1.663 0.0978 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1367 on 207 degrees of freedom
Multiple R-squared: 0.01319, Adjusted R-squared: 0.008421
F-statistic: 2.767 on 1 and 207 DF, p-value: 0.09777Python
1281.1196172248804Python
# OLS model
X = data['roe']
X = sm.add_constant(X)
y = data['salary']
model = sm.OLS(y, X).fit() # Fit the linear regression model
salaryhat = model.fittedvalues # Predicted values for the dependent variable
uhat = model.resid # Predict regression residuals
salarymean = pd.Series([y.mean()] * len(y)) # Generating the mean of salary
print(model.summary()) OLS Regression Results
==============================================================================
Dep. Variable: salary R-squared: 0.013
Model: OLS Adj. R-squared: 0.008
Method: Least Squares F-statistic: 2.767
Date: ter, 30 jan 2024 Prob (F-statistic): 0.0978
Time: 15:41:07 Log-Likelihood: -1804.5
No. Observations: 209 AIC: 3613.
Df Residuals: 207 BIC: 3620.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 963.1913 213.240 4.517 0.000 542.790 1383.592
roe 18.5012 11.123 1.663 0.098 -3.428 40.431
==============================================================================
Omnibus: 311.096 Durbin-Watson: 2.105
Prob(Omnibus): 0.000 Jarque-Bera (JB): 31120.902
Skew: 6.915 Prob(JB): 0.00
Kurtosis: 61.158 Cond. No. 43.3
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.Stata
Variable | Obs Mean Std. dev. Min Max
-------------+---------------------------------------------------------
salary | 209 1281.12 1372.345 223 14822
Source | SS df MS Number of obs = 209
-------------+---------------------------------- F(1, 207) = 2.77
Model | 5166419.04 1 5166419.04 Prob > F = 0.0978
Residual | 386566563 207 1867471.32 R-squared = 0.0132
-------------+---------------------------------- Adj R-squared = 0.0084
Total | 391732982 208 1883331.64 Root MSE = 1366.6
------------------------------------------------------------------------------
salary | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
roe | 18.50119 11.12325 1.66 0.098 -3.428196 40.43057
_cons | 963.1913 213.2403 4.52 0.000 542.7902 1383.592
------------------------------------------------------------------------------Goodness-of-fit
R
library(foreign) # importing dataset from a stata dta file
mydata <- read.dta("files/CEOSAL1.dta")
attach(mydata)
model <- lm(salary ~ roe)
salaryhat <- fitted(model) # Predict values for dependent variable
uhat <- resid(model) # Predict regression residuals
salarymean <- rep(mean(salary),length(salary)) # Generating the mean of salary
# r-squared is simply the ratio of portion explained over total that could be explained - Understanding what SSR, SSE and SST mean
plot(salary ~ roe)
abline(lm(salary ~ roe), col = "blue")
abline(lm(salarymean ~ roe), col = "red")
Python
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
data = pd.read_stata("files/CEOSAL1.dta")
X = data[['roe']]
y = data['salary']
salarymean = np.repeat(y.mean(), len(y))
X_mean = X.mean()
y_mean = y.mean()
slope = np.sum((X - X_mean) * (y - y_mean)) / np.sum((X - X_mean) ** 2)
intercept = y_mean - slope * X_mean
salaryhat = slope * X + intercept
# Plotting the data and regression lines
plt.scatter(X, y, alpha=0.7)
plt.plot(X, salaryhat, color='blue', linewidth=2)
plt.plot(X, salarymean, color='red', linewidth=2)
plt.xlabel('roe')
plt.ylabel('salary')
plt.show()
Goodness-of-fit
Manually calculating \(R^2\)
R
library(foreign) # importing dataset from a stata dta file
mydata <- read.dta("files/CEOSAL1.dta")
attach(mydata)
model <- lm(salary ~ roe)
salaryhat <- fitted(model) # Predict values for dependent variable
uhat <- resid(model) # Predict regression residuals
salarymean <- rep(mean(salary),length(salary)) # Generating the mean of salary
# r-squared is simply the ratio of portion explained over total that could be explained
ssr <- sum(uhat^2)
ssrB <- sum((salary - salaryhat)^2)
sst <- sum((salary - salarymean)^2)
sse <- sum((salaryhat - salarymean)^2)
sse / sst[1] 0.01318862Python
import pandas as pd
import numpy as np
import statsmodels.api as sm
data = pd.read_stata("files/CEOSAL1.dta")
X = data['roe']
y = data['salary']
X = sm.add_constant(X) # Add a constant term (intercept)
model = sm.OLS(y, X).fit()
salaryhat = model.fittedvalues
uhat = model.resid
salarymean = np.repeat(y.mean(), len(y))
# Calculate R-squared
ssr = np.sum(uhat**2)
ssrB = np.sum((y - salaryhat)**2)
sst = np.sum((y - salarymean)**2)
sse = np.sum((salaryhat - salarymean)**2)
rsquared = sse / sst
print(rsquared)0.013188624081034118Stata
.01318862Variance of coefficients
Variance of coefficients
When we estimate coefficients we have some “error of estimation”.
Basically, you are searching the “true” coefficient using a sample, which should be representative of the population but it is not the population itself.
This means that the coefficient estimated is estimated with error.
We would like (e.g., we will need) to impose some “structure” to that error.
Variance of coefficients
Standard error and T-stat
To assess if the variables are significantly related, you need to assess the significance of \(\beta\) coefficients.
Using the example from Wooldridge, we know that the Beta of ROE is 18.591, while the standard error of ROE is 11.123.
The standard error is a measure of the accuracy of your estimate. If you find a large standard error, your estimate does not have good accuracy.
Ideally, you would find small standard errors, meaning that your coefficient is accurately estimated.
However, you do not have good control over the magnitude of the standard errors.
Variance of coefficients
Standard error and T-stat
If you have a large standard error, probably you coefficient will not be significantly different from zero. You can test whether your coefficient is significantly different from zero computing the t-statistics as follows:
\[t_{\beta} = \frac{\hat{\beta}}{se(\hat{\beta})}\]
If \(t_{\beta}\) is large enough, you can say that \(\beta\) is significantly different from zero. Usually, \(t_{\beta}\) larger than 2 is enough to be significant.
Variance of coefficients
In the previous example, you can find the t-stat manually as follows (\(t_{\beta} =\frac{\hat{\beta}}{se(\hat{\beta})}\)):
Python
import pandas as pd
import statsmodels.api as sm
data = pd.read_stata("files/CEOSAL1.dta")
# OLS model
X = data['roe']
X = sm.add_constant(X)
y = data['salary']
model = sm.OLS(y, X).fit()
# Extract and calculate specific coefficients
coef_beta = model.params['roe']
coef_std_error = model.bse['roe']
# Calculate t-value
t_value = coef_beta / coef_std_error
# Print the coefficient and t-value
print("Coefficient (beta):", coef_beta)Coefficient (beta): 18.501186345214933Standard Error: 11.123250903287634t-value: 1.6632894920806511Stata
Coefficient (beta): 18.501186
Standard Error: 11.123251
t-value: 1.6632895Variance of coefficients
Naturally, the previous analysis requires an estimate of \(\beta\) and an estimate of the \(\beta\)’s standard error.
The standard error can be defined as:
\[se(\hat{\beta_1})=\frac{\hat{\sigma}}{\sqrt{SST_x}}\]
- Where \(\hat{\sigma}\) is the standard deviation of the error term in the regression, which can be calculated as:
\[\hat{\sigma} = \sqrt{\frac{SSR}{n-2}}\]
- The $n-2$ here is an adjustment for the degrees of freedom in the regression.- SST is defined as before \(\sum_i^n(y_i-\hat{y_i})^2\)
Variance of coefficients
R
[1] 11.12325R
#calculating manually
# Extract the residuals
residuals <- resid(model)
# Number of observations (n)
n <- length(residuals)
# Calculate the mean of the independent variable (roe)
roe_mean <- mean(roe)
# Calculate the sum of squared deviations of roe from its mean (SXX)
SST <- sum((roe - roe_mean)^2)
# Calculate the sum of squared errors (SSE)
SSR <- sum(residuals^2)
# Calculate the standard error of beta
Sd_beta <- sqrt(SSR / ((n - 2)))
# Calculate S.E
Se_beta <- Sd_beta / sqrt(SST)
# Print the standard error of beta
print(Se_beta)[1] 11.12325Python
import pandas as pd
import numpy as np
import statsmodels.api as sm
data = pd.read_stata("files/CEOSAL1.dta")
X = data['roe']
y = data['salary']
X = sm.add_constant(X)
model = sm.OLS(y, X).fit()
# Extract the standard error of the coefficient for 'roe'
beta_se_summary = model.bse['roe']
print("Standard Error (from summary):", beta_se_summary)Standard Error (from summary): 11.123250903287634Python
# Calculate it manually
# Extract the residuals
residuals = model.resid
# Number of observations (n)
n = len(residuals)
# Calculate the mean of the independent variable (roe)
roe_mean = X['roe'].mean()
# Calculate the sum of squared deviations of roe from its mean (SST)
SST = np.sum((X['roe'] - roe_mean) ** 2)
# Calculate the sum of squared errors (SSE)
SSE = np.sum(residuals ** 2)
# Calculate the standard error of beta (Sd_beta)
Sd_beta = np.sqrt(SSE / (n - 2))
# Calculate SE_beta
SE_beta = Sd_beta / np.sqrt(SST)
print("Standard Error (manually calculated):", SE_beta)Standard Error (manually calculated): 11.123250601798315Stata
use "files/CEOSAL1.DTA" , replace
qui reg salary roe
gen beta_se_summary = _se[roe]
gen n = _N
predict residuals, residuals
sum roe, meanonly
gen roe_diff = roe - r(mean)
egen roe_diff_sq = total(roe_diff^2)
gen residuals_sq = residuals^2
egen residuals_sq_sum = total(residuals_sq)
gen Sd_beta = sqrt(residuals_sq_sum / (n - 2))
gen SE_beta = Sd_beta / sqrt(roe_diff_sq)
display "Standard Error (from summary): " sum(beta_se_summary)
display "Standard Error (manually calculated): " sum(SE_beta)Standard Error (from summary): 11.123251
Standard Error (manually calculated): 11.123251Variance of coefficients
Another comment:
\[se(\hat{\beta_1})=\frac{\hat{\sigma}}{\sqrt{SST_x}}\]
The larger \(\hat{\sigma}\) is, the larger the variance of \(\beta\). That is, the more “noise” in the association between x and Y, the harder it is to learn something about \(\beta\).
However, more variation in x, the larger the SST, so the smaller is the variance of \(\beta\).
Robust standard errors
Robust standard errors
Looking at both equations below:
\[t_{\beta} = \frac{\hat{\beta}}{se(\hat{\beta})}\]
\[se(\hat{\beta_1})=\frac{\hat{\sigma}}{\sqrt{SST_x}}\]
What happens if \(\hat{\sigma}\) is not constant (for the values of x)?
In other words, how realistic is to assume that the variance in the errors is the same for all slices of x?
Can you think of an example where that may happen?
Robust standard errors
Earnings = f(education)
PhD have a higher variance of earnings than non-educated people.
Leveragge=f(Size)
It is quite possible that small firms will have less options of leverage than large companies.
This means that a sub-sample of large companies will have higher variance in the leverage decisions (and thus the error terms) than the sub-sample of small firms
Robust standard errors
One of the key assumptions in OLS estimators is homoscedasticity
That is, the assumption is that the variance of the errors is homoscedastic (constant variance in all slices of X).
It means that throughout all observations, the error term shows the same variance.
If errors are not homoscedastic, we have the heteroscedasticity problem.
Heteroskedasticity does not cause bias or inconsistency in the OLS estimators of the \(\beta\) like the OVB would.
It also does not affect the \(R^2\).
What Heteroscedasticity does is to bias the standard errors of the estimates.
Robust standard errors
Robust standard errors
Robust standard errors
Homoskedascticity = Constant \(\hat{\sigma}\) to all slices of X.
Heteroskedascticity = Non-constant \(\hat{\sigma}\) to all slices of X.
Without homoskedascticity, OLS no longer has the minimum mean squared errors, which means that the estimated standard errors are biased, which in turn creates bias in the t-stat and the inference you’ll make with your model.
Fortunately, we have an easy solution for that.
\[Var(\hat{\beta_1}) = \frac{\sum_i^n(x_i-\bar{x})^2\hat{\mu}^2}{SST^2_x}\]
This formula simply “includes” the heteroskedascticity in the calculation of \(Var(\hat{\beta_1})\), meaning this correct the estimated standard deviation to heteroskedascticity.
We call this correction as Robust Standard Errors (White Robust).
In other words, you should always use Robust Standard Errors. It is easy to use it with R.
Robust standard errors
Using Robust Standard-errors.
R
library(sandwich)
library(foreign)
library(lmtest)
data <- read.dta("files/CEOSAL1.DTA")
model <- lm(salary ~ roe, data = data)
robust_model <- coeftest(model, vcov = vcovHC(model, type = "HC3"))
SE_beta_robust <- robust_model["roe", "Std. Error"]
cat("Robust Standard Error :", SE_beta_robust, "\n")Robust Standard Error : 6.899434 Python
Robust Standard Error : 6.899433834797476Stata
Standard Error (non-robust): 11.123251
Standard Error (robust): 6.8294482Robust standard errors
Notice that the standard errors have changed quite significantly in this example.
Usually, the robust standard errors are larger than the traditional ones in empirical works.
But, in this example, they are smaller.
Perhaps more importantly:
Once the S.e. change, you should expect that the t-stat of the estimates also change.
Final comment: robust standard errors are robust in the case of homoskedasticity.
Warning
Thus, you should always use robust S.E.
Clustered standard errors
Clustered standard errors
Almost always, someone will ask you whether you clustered your standard errors.
The intuition is the following:
When you do not cluster, you are assuming that all observations are independently and identically distributed (i.i.d.), which may or may not be true.
Imagine you are studying the effect of class size on students achievement.
How much of a effect would have the teacher of a class?
In this design, the teacher influences the achievement of all the students in the same class, and one teacher cannot be at two classes at the same time.
Thus, it would be wise to cluster the errors at the class-level. This assumes that the residual of each individual is clustered with the other individuals in the same class.
In principle, clustering solves any form of dependence of the residuals in your data.
Clustered standard errors
In corporate finance/accounting research panel data research, the tradition is to cluster at the firm-level.
- The reason is that the observations of the same firm are not independent trough time, thus are correlated.
But, there is a lot of debate about this decision.
The tip is to cluster where the randomness exist. That is quite subjective. In the class size example, the randomness comes out of the teacher, since each teacher has their own ways of teaching (materials, resources, etc.).
But, it is a good practice to stress this decision a bit in your own research by also showing results with clustered s.e. at the industry-level.
Final tip: usually the minimum number of cluster is about 30. Less than that might be insufficient (but, again, the guidance in this topic is very subjective).
Clustered standard errors
The clustered standard errors are different because I am fabricating the clusters here for the sake of the coding.
In your real research, you would have the cluster at hands.
R
library(sandwich)
library(foreign)
library(lmtest)
library(plm)
data <- read.dta("files/CEOSAL1.DTA")
model <- lm(salary ~ roe, data = data)
robust_model <- coeftest(model, vcov = vcovHC(model, type = "HC3"))
#clustered
data$cluster <- rep(1:35, length.out = nrow(data))
model <- plm(salary ~ roe, data = data, index = c("cluster"))
clustered_se <- vcovHC(model, type = "HC3", cluster = "group")
SE_beta_clustered <- sqrt(clustered_se["roe", "roe"])
cat("Standard Error (robust):", SE_beta_robust, "\n")Standard Error (robust): 6.899434 Standard Error (clustered):: 12.98492 Python
Length of values (175) does not match length of index (209)Python
'numpy.ndarray' object has no attribute 'loc'Python
'cluster'Python
name 'model_clustered' is not definedRobust Standard Error (HC3): 6.899433834797476name 'clustered_se' is not definedStata
use "files/CEOSAL1.DTA" , replace
qui reg salary roe
gen beta_se_non = _se[roe]
qui reg salary roe , robust
gen beta_se_summary = _se[roe]
egen cluster = seq(), block(6)
qui regress salary roe , vce(cluster cluster)
gen SE_beta_clustered = _se[roe]
di "Standard Error (non-robust): " sum(beta_se_non)
di "Standard Error (robust): " sum(beta_se_summary)
di "Standard Error (clustered): " sum(SE_beta_clustered)Standard Error (non-robust): 11.123251
Standard Error (robust): 6.8294482
Standard Error (clustered): 6.4122176Panel Data
Panel Data
As explained previously, OVB is a significant source of “endogeneity” in empirical research.
OVB is a problem because of the considerable heterogeneity in many empirical settings.
Many of the omitted variables are unobservable to the researcher.
Panel data can sometimes offer a partial.
Panel Data
We start defining the following:
\[y_{i,t} = \alpha + \beta_1 x_{i,t} + \epsilon_{i,t}\]
Where:
- \(i = 1, . . . , N\)
- \(t = 1, . . . , T\)
Imagine that the residual can be decomposed in:
\[\epsilon_{i,t} = c_i + \mu_{i,t}\]
The term \(c_i\) is constant.
Panel Data
The term \(c_i\) is constant.
It captures the aggregate effect of all of the unobservable, time-invariant explanatory variables for \(y_{it}\).
To focus attention on the issues specific to panel data, we assume that \(e_{it}\) has a zero mean conditional on \(x_{it}\) and \(c_i\) for all \(t\).
The most important thing here is whether \(x_{it}\) and \(c_i\) are correlated.
Why?
Panel Data
The most important thing here is whether \(x_{it}\) and \(c_i\) are correlated.
If \(x_{it}\) and \(c_i\) are correlated, then \(c_i\) is referred to as a “fixed effect”.
- It there is correlation, there is violation of the Conditional Mean Independence (CMI) assumption.
If \(x_{it}\) and \(c_i\) are not correlated, then \(c_i\) is referred to as a “random effect”.
- Endogeneity is not a concern; however, the computation of standard errors is affected.
Panel Data
Why might fixed effects arise?
FE are any time-invariant unit characteristic that cannot be observed in the data.
- education level,
- firm’s culture,
- technology,
- managerial talent,
- investment opportunities,
- location (economic development, institutions, etc.),
- etc.
Panel Data
We say things like (you have to understand that they refer to FE):
- “Time-invariant heterogeneity at the unit-level”
- “Unobserved variation that occur at the unit-level that do not vary over time”
Important: with FE, you are capturing all unobserved heterogeneity that do not vary over time.
Panel Data
Definition of Panel Data:
You have multiple observations per unit (individual, firm, etc.)
In datasets, it is “one panel below the other” not “one panel beside the other”.
Four main topics in Panel Data:
Pooled cross-sectional
Fixed Effect models (including multidimensional FE)
Random Effects model
First differences
Lagged models
Panel Data
Formal definition
\[y_{i,t} = \alpha + \beta_1 x_{i,t} + \delta FE + \epsilon_{i,t}\]
\(E(\epsilon_{i,t}) = 0\)
\(corr(x_{i,t},FE) \neq 0\)
\(corr(FE, \epsilon_{i,t}) = 0\)
\(corr(x_{i,t},epsilon_{i,t}) = 0\), for all t
The last assumption is called strict exogeneity assumption and means that the residual of any t is uncorrelated with x of any t.
That is, under a strict exogeneity assumption on the explanatory variables, the fixed effects estimator is unbiased: the idiosyncratic error should be uncorrelated with each explanatory variable across all time periods.
Remember that if we ignore FE, we have OVB.
Panel Data
Before we continue…
Comment #1
The standard errors in this framework must be “clustered” by panel unit (e.g., individual) to allow for correlation in the residual for the same person over time. This yields valid inference as long as the number of clusters is “large.”
Comment #2
FE cannot solve reverse causality, it might help you with OVB.
Comment #3
Three main types of FE:
- Pooled
- Within-transformation (when someone says FE, it is usually this one)
- Random Effects
Pooling Cross-sections
Pooling Cross-Sections
When you have two periods of the same unit, but the periods are not consecutive, you have a pooled cross-sectional data.
This is common in survey data.
If you use only one period, you might find biased results.
Let’s practice with the dataset CRIME2 from Wooldridge.
This dataset contains data (many cities) on the crime rate, unemployment rate and many other city-related variables.
There are two years, 82 and 87 (this is pooled cross-section).
Pooling Cross-Sections
If we estimate only using the year 87, we would interpret that unemployment leads to lower crime rate.
R
Call:
lm(formula = crmrte ~ unem, data = data1)
Residuals:
Min 1Q Median 3Q Max
-57.55 -27.01 -10.56 18.01 79.75
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 128.378 20.757 6.185 1.8e-07 ***
unem -4.161 3.416 -1.218 0.23
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 34.6 on 44 degrees of freedom
Multiple R-squared: 0.03262, Adjusted R-squared: 0.01063
F-statistic: 1.483 on 1 and 44 DF, p-value: 0.2297Python
OLS Regression Results
==============================================================================
Dep. Variable: crmrte R-squared: 0.033
Model: OLS Adj. R-squared: 0.011
Method: Least Squares F-statistic: 1.483
Date: ter, 30 jan 2024 Prob (F-statistic): 0.230
Time: 15:41:25 Log-Likelihood: -227.27
No. Observations: 46 AIC: 458.5
Df Residuals: 44 BIC: 462.2
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 128.3781 20.757 6.185 0.000 86.546 170.210
unem -4.1611 3.416 -1.218 0.230 -11.047 2.724
==============================================================================
Omnibus: 3.902 Durbin-Watson: 1.106
Prob(Omnibus): 0.142 Jarque-Bera (JB): 3.681
Skew: 0.641 Prob(JB): 0.159
Kurtosis: 2.473 Cond. No. 25.3
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified. Source | SS df MS Number of obs = 46
-------------+---------------------------------- F(1, 44) = 1.48
Model | 1775.90928 1 1775.90928 Prob > F = 0.2297
Residual | 52674.6428 44 1197.15097 R-squared = 0.0326
-------------+---------------------------------- Adj R-squared = 0.0106
Total | 54450.5521 45 1210.01227 Root MSE = 34.6
------------------------------------------------------------------------------
crmrte | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
unem | -4.161134 3.416456 -1.22 0.230 -11.04655 2.72428
_cons | 128.3781 20.75663 6.18 0.000 86.54589 170.2104
------------------------------------------------------------------------------Pooling Cross-Sections
When we consider a panel, we get the expected positive sign. This is evidence that the previous model suffered from OVB. Still, the coefficient of unem is not significant probably because of time-invariant unobserved heterogeneity in the cities.
R
Call:
lm(formula = crmrte ~ d87 + unem, data = data)
Residuals:
Min 1Q Median 3Q Max
-53.474 -21.794 -6.266 18.297 75.113
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 93.4203 12.7395 7.333 9.92e-11 ***
d87 7.9404 7.9753 0.996 0.322
unem 0.4265 1.1883 0.359 0.720
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 29.99 on 89 degrees of freedom
Multiple R-squared: 0.01221, Adjusted R-squared: -0.009986
F-statistic: 0.5501 on 2 and 89 DF, p-value: 0.5788Python
OLS Regression Results
==============================================================================
Dep. Variable: crmrte R-squared: 0.012
Model: OLS Adj. R-squared: -0.010
Method: Least Squares F-statistic: 0.5501
Date: ter, 30 jan 2024 Prob (F-statistic): 0.579
Time: 15:41:27 Log-Likelihood: -441.90
No. Observations: 92 AIC: 889.8
Df Residuals: 89 BIC: 897.4
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 93.4203 12.739 7.333 0.000 68.107 118.733
d87 7.9404 7.975 0.996 0.322 -7.906 23.787
unem 0.4265 1.188 0.359 0.720 -1.935 2.788
==============================================================================
Omnibus: 8.350 Durbin-Watson: 1.157
Prob(Omnibus): 0.015 Jarque-Bera (JB): 8.771
Skew: 0.756 Prob(JB): 0.0125
Kurtosis: 2.935 Cond. No. 40.1
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified. Source | SS df MS Number of obs = 92
-------------+---------------------------------- F(2, 89) = 0.55
Model | 989.717314 2 494.858657 Prob > F = 0.5788
Residual | 80055.7864 89 899.503218 R-squared = 0.0122
-------------+---------------------------------- Adj R-squared = -0.0100
Total | 81045.5037 91 890.609931 Root MSE = 29.992
------------------------------------------------------------------------------
crmrte | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
d87 | 7.940413 7.975324 1.00 0.322 -7.906386 23.78721
unem | .4265461 1.188279 0.36 0.720 -1.934539 2.787631
_cons | 93.42026 12.73947 7.33 0.000 68.1072 118.7333
------------------------------------------------------------------------------Pooling Cross-Sections
This shows us that we should also control for the year variable.
We call this, Year Fixed Effects.
We still most likely have OVB due to the unobserved heterogeneity in cities, that is, we still would need to include cities FE.
Demeaned variables
Demeaned variables
A first way to eliminate the FE is by demeaning the data.
Consider the following:
\[\bar{y_i} = \alpha +\beta \bar{x_i} + \delta FE + \bar{\epsilon_i}\]
\[\frac{1}{T}\sum{y_{i,t}} = \alpha +\beta \frac{1}{T}\sum{x_{i,t}} + \delta FE + \frac{1}{T}\sum{\epsilon_{i,t}}\]
If we subtract the mean of each variable, we have:
\[(y_{i,t} - \bar{y_i}) = \beta (x_{i,t} - \bar{x_i}) + (\epsilon_{i,t} - \bar{\epsilon_i})\]
Because the FE does not vary over time, each value is equal to the mean.
Thus, when you demean, you eliminate the FE from the equation. You also eliminate the intercept \(\alpha\).
Takeaway: OLS will estimate unbiased coefficients if you demean the variables.
This is called within-transformation because you are demeaning “within” the group.
Demeaned variables
Let’s use the dataset WAGEPAN to estimate the following equation.
\[Ln(wage)=\alpha + \beta_1 exper^2 + \beta_2 married + \beta_3 union + \epsilon\]
Some variables in the dataset do not vary over time. These variables cannot be included in this equation.
Demeaned variables
See page 495 Wooldridge.
R
library(foreign)
library(stargazer)
library(sandwich)
data <- read.dta("files/WAGEPAN.dta")
# Calculate mean by nr for lwage, expersq, married, and union
data <- data[order(data$nr), ] # Sort data by nr for by-group operations
data$lwage_mean <- ave(data$lwage, data$nr, FUN = mean)
data$expersq_mean <- ave(data$expersq, data$nr, FUN = mean)
data$married_mean <- ave(data$married, data$nr, FUN = mean)
data$union_mean <- ave(data$union, data$nr, FUN = mean)
data$lwage_demean <- data$lwage - data$lwage_mean
data$expersq_demean <- data$expersq - data$expersq_mean
data$married_demean <- data$married - data$married_mean
data$union_demean <- data$union - data$union_mean
model1 <- lm(lwage ~ educ + black + hisp + exper + expersq + married + union + d81 + d82 + d83 + d84 + d85 + d86 + d87, data = data)
model2 <- lm(lwage_demean ~ expersq_demean + married_demean + union_demean + d81 + d82 + d83 + d84 + d85 + d86 + d87, data = data)
stargazer(model1, model2 ,title = "Regression Results", column.labels=c("OLS","Demean"), type = "text")
Regression Results
=======================================================================
Dependent variable:
---------------------------------------------------
lwage lwage_demean
OLS Demean
(1) (2)
-----------------------------------------------------------------------
educ 0.091***
(0.005)
black -0.139***
(0.024)
hisp 0.016
(0.021)
exper 0.067***
(0.014)
expersq -0.002***
(0.001)
married 0.108***
(0.016)
union 0.182***
(0.017)
expersq_demean -0.005***
(0.001)
married_demean 0.047***
(0.017)
union_demean 0.080***
(0.018)
d81 0.058* 0.151***
(0.030) (0.021)
d82 0.063* 0.253***
(0.033) (0.023)
d83 0.062* 0.354***
(0.037) (0.027)
d84 0.090** 0.490***
(0.040) (0.034)
d85 0.109** 0.617***
(0.043) (0.042)
d86 0.142*** 0.765***
(0.046) (0.053)
d87 0.174*** 0.925***
(0.049) (0.064)
Constant 0.092 -0.445***
(0.078) (0.030)
-----------------------------------------------------------------------
Observations 4,360 4,360
R2 0.189 0.181
Adjusted R2 0.187 0.179
Residual Std. Error 0.480 (df = 4345) 0.328 (df = 4349)
F Statistic 72.459*** (df = 14; 4345) 95.840*** (df = 10; 4349)
=======================================================================
Note: *p<0.1; **p<0.05; ***p<0.01Python
import pandas as pd
import statsmodels.api as sm
import statsmodels.formula.api as smf
from statsmodels.iolib.summary2 import summary_col
data = pd.read_stata("files/WAGEPAN.dta")
data = data.sort_values(by='nr') # Sort data by nr for by-group operations
data['lwage_mean'] = data.groupby('nr')['lwage'].transform('mean')
data['expersq_mean'] = data.groupby('nr')['expersq'].transform('mean')
data['married_mean'] = data.groupby('nr')['married'].transform('mean')
data['union_mean'] = data.groupby('nr')['union'].transform('mean')
data['lwage_demean'] = data['lwage'] - data['lwage_mean']
data['expersq_demean'] = data['expersq'] - data['expersq_mean']
data['married_demean'] = data['married'] - data['married_mean']
data['union_demean'] = data['union'] - data['union_mean']
model1 = sm.OLS(data['lwage'], sm.add_constant(data[['educ', 'black', 'hisp', 'exper', 'expersq', 'married', 'union', 'd81', 'd82', 'd83', 'd84', 'd85', 'd86', 'd87']])).fit()
model2 = sm.OLS(data['lwage_demean'], sm.add_constant(data[['expersq_demean', 'married_demean', 'union_demean', 'd81', 'd82', 'd83', 'd84', 'd85', 'd86', 'd87']])).fit()
# Display regression results using stargazer
summary = summary_col([model1, model2], stars=True)
print(summary)
======================================
lwage lwage_demean
--------------------------------------
R-squared 0.1893 0.1806
R-squared Adj. 0.1867 0.1787
black -0.1392***
(0.0236)
const 0.0921 -0.4446***
(0.0783) (0.0297)
d81 0.0583* 0.1512***
(0.0304) (0.0205)
d82 0.0628* 0.2530***
(0.0332) (0.0228)
d83 0.0620* 0.3544***
(0.0367) (0.0274)
d84 0.0905** 0.4901***
(0.0401) (0.0339)
d85 0.1092** 0.6175***
(0.0434) (0.0423)
d86 0.1420*** 0.7655***
(0.0464) (0.0525)
d87 0.1738*** 0.9250***
(0.0494) (0.0643)
educ 0.0913***
(0.0052)
exper 0.0672***
(0.0137)
expersq -0.0024***
(0.0008)
expersq_demean -0.0052***
(0.0007)
hisp 0.0160
(0.0208)
married 0.1083***
(0.0157)
married_demean 0.0467***
(0.0171)
union 0.1825***
(0.0172)
union_demean 0.0800***
(0.0181)
======================================
Standard errors in parentheses.
* p<.1, ** p<.05, ***p<.01Stata
use "files/WAGEPAN.dta" , clear
bys nr: egen lwage_mean = mean(lwage)
bys nr: egen expersq_mean = mean(expersq)
bys nr: egen married_mean = mean(married)
bys nr: egen union_mean = mean(union)
gen lwage_demean = lwage - lwage_mean
gen expersq_demean = expersq - expersq_mean
gen married_demean = married - married_mean
gen union_demean = union - union_mean
eststo: qui reg lwage educ black hisp exper expersq married union d81 d82 d83 d84 d85 d86 d87
eststo: qui reg lwage_demean expersq_demean married_demean union_demean d81 d82 d83 d84 d85 d86 d87
esttab , mtitles("OLS" "Demean") compress(est1 stored)
(est2 stored)
------------------------------------
(1) (2)
OLS Demean
------------------------------------
educ 0.0913***
(17.44)
black -0.139***
(-5.90)
hisp 0.0160
(0.77)
exper 0.0672***
(4.91)
expersq -0.00241**
(-2.94)
married 0.108***
(6.90)
union 0.182***
(10.63)
d81 0.0583 0.151***
(1.92) (7.36)
d82 0.0628 0.253***
(1.89) (11.08)
d83 0.0620 0.354***
(1.69) (12.96)
d84 0.0905* 0.490***
(2.26) (14.46)
d85 0.109* 0.617***
(2.52) (14.59)
d86 0.142** 0.765***
(3.06) (14.58)
d87 0.174*** 0.925***
(3.52) (14.38)
expe~emean -0.00519***
(-7.87)
marr~emean 0.0467**
(2.73)
union_de~n 0.0800***
(4.43)
_cons 0.0921 -0.445***
(1.18) (-14.96)
------------------------------------
N 4360 4360
------------------------------------
t statistics in parentheses
* p<0.05, ** p<0.01, *** p<0.001Practical Tips
Practical Tips
You will not need to demean the variables every time you want to estimate a fixed effect models.
The statistical softwares have packages that do that.
You only need to know that Fixed effects model is a demeaned model, i.e., a within-transformation model.
But notice that you will have many different Fixed Effects together:
- Firm Fixed Effects
- Year Fixed Effects
- Individual Fixed Effects (if individuals change between firms)
I am calling a multidimensional fixed effects design if you expand the FE to interactions of FE. Most common:
- Year-Industry Fixed Effects.
- CEO-Firm Fixed Effects.
Practical Tips
Notice the number of dummies in the last two columns.
R
library(foreign)
library(stargazer)
library(sandwich)
library(plm)
data <- read.dta("files/WAGEPAN.dta")
# Calculate mean by nr for lwage, expersq, married, and union
data <- data[order(data$nr), ] # Sort data by nr for by-group operations
data$lwage_mean <- ave(data$lwage, data$nr, FUN = mean)
data$expersq_mean <- ave(data$expersq, data$nr, FUN = mean)
data$married_mean <- ave(data$married, data$nr, FUN = mean)
data$union_mean <- ave(data$union, data$nr, FUN = mean)
data$lwage_demean <- data$lwage - data$lwage_mean
data$expersq_demean <- data$expersq - data$expersq_mean
data$married_demean <- data$married - data$married_mean
data$union_demean <- data$union - data$union_mean
# set panel data
pdata <- pdata.frame(data, index = c("nr", "year"))
# Random effects regression using plm
model_de <- lm(lwage_demean ~ expersq_demean + married_demean + union_demean + d81 +d82+ d83+ d84+ d85 +d86 +d87 , data = data)
model_fe <- plm(lwage ~ expersq + married + union + factor(year) + educ + black + hisp + exper, data = pdata, model = "within")
model_du <- lm( lwage ~ expersq + married + union + factor(year) + factor(nr) + educ + black + hisp + exper, data = data)
# Display regression results using stargazer
#summary(model_de)
#summary(model_fe)
#summary(model_du)
stargazer(model_de, model_fe, model_du ,title = "Regression Results", type = "text")
Regression Results
==================================================================================================
Dependent variable:
------------------------------------------------------------------------------
lwage_demean lwage
OLS panel OLS
linear
(1) (2) (3)
--------------------------------------------------------------------------------------------------
expersq_demean -0.005***
(0.001)
married_demean 0.047***
(0.017)
union_demean 0.080***
(0.018)
d81 0.151***
(0.021)
d82 0.253***
(0.023)
d83 0.354***
(0.027)
d84 0.490***
(0.034)
d85 0.617***
(0.042)
d86 0.765***
(0.053)
d87 0.925***
(0.064)
expersq -0.005*** -0.005***
(0.001) (0.001)
married 0.047** 0.047**
(0.018) (0.018)
union 0.080*** 0.080***
(0.019) (0.019)
factor(year)1981 0.151*** 0.151***
(0.022) (0.022)
factor(year)1982 0.253*** 0.253***
(0.024) (0.024)
factor(year)1983 0.354*** 0.354***
(0.029) (0.029)
factor(year)1984 0.490*** 0.490***
(0.036) (0.036)
factor(year)1985 0.617*** 0.617***
(0.045) (0.045)
factor(year)1986 0.765*** 0.765***
(0.056) (0.056)
factor(year)1987 0.925*** 0.925***
(0.069) (0.069)
factor(nr)17 0.579***
(0.177)
factor(nr)18 0.929***
(0.179)
factor(nr)45 0.554***
(0.176)
factor(nr)110 1.046***
(0.180)
factor(nr)120 0.239
(0.176)
factor(nr)126 0.783***
(0.176)
factor(nr)150 -0.140
(0.176)
factor(nr)162 0.269
(0.176)
factor(nr)166 0.138
(0.176)
factor(nr)189 0.191
(0.176)
factor(nr)193 0.981***
(0.176)
factor(nr)209 0.707***
(0.176)
factor(nr)212 0.833***
(0.176)
factor(nr)218 1.231***
(0.176)
factor(nr)243 0.586***
(0.178)
factor(nr)259 0.478***
(0.177)
factor(nr)260 0.789***
(0.176)
factor(nr)309 1.052***
(0.177)
factor(nr)351 0.358**
(0.177)
factor(nr)353 0.583***
(0.176)
factor(nr)383 0.564***
(0.176)
factor(nr)408 0.801***
(0.177)
factor(nr)424 1.345***
(0.181)
factor(nr)464 0.080
(0.176)
factor(nr)483 0.713***
(0.179)
factor(nr)556 1.089***
(0.176)
factor(nr)560 0.205
(0.176)
factor(nr)569 -0.431**
(0.176)
factor(nr)583 0.852***
(0.178)
factor(nr)647 0.360**
(0.177)
factor(nr)658 0.838***
(0.177)
factor(nr)684 1.132***
(0.176)
factor(nr)711 -0.097
(0.176)
factor(nr)729 0.837***
(0.176)
factor(nr)731 0.574***
(0.178)
factor(nr)732 0.531***
(0.176)
factor(nr)793 0.498***
(0.176)
factor(nr)797 0.841***
(0.177)
factor(nr)800 0.380**
(0.176)
factor(nr)813 -0.657***
(0.176)
factor(nr)823 -0.393**
(0.176)
factor(nr)827 0.507***
(0.176)
factor(nr)847 0.489***
(0.176)
factor(nr)851 0.735***
(0.176)
factor(nr)863 0.550***
(0.176)
factor(nr)873 -0.127
(0.176)
factor(nr)891 0.735***
(0.176)
factor(nr)908 -0.405**
(0.176)
factor(nr)910 0.679***
(0.176)
factor(nr)916 0.564***
(0.176)
factor(nr)919 0.238
(0.178)
factor(nr)922 1.011***
(0.176)
factor(nr)924 -0.071
(0.176)
factor(nr)925 0.809***
(0.176)
factor(nr)944 0.106
(0.176)
factor(nr)945 0.106
(0.176)
factor(nr)947 1.154***
(0.177)
factor(nr)955 1.006***
(0.178)
factor(nr)965 0.434**
(0.180)
factor(nr)996 0.007
(0.177)
factor(nr)1007 0.996***
(0.177)
factor(nr)1054 0.133
(0.177)
factor(nr)1064 0.858***
(0.179)
factor(nr)1081 0.179
(0.176)
factor(nr)1085 0.114
(0.176)
factor(nr)1091 0.226
(0.183)
factor(nr)1094 0.600***
(0.177)
factor(nr)1096 0.251
(0.182)
factor(nr)1098 0.837***
(0.176)
factor(nr)1102 0.948***
(0.176)
factor(nr)1107 0.762***
(0.180)
factor(nr)1142 0.715***
(0.176)
factor(nr)1156 0.569***
(0.179)
factor(nr)1180 0.636***
(0.176)
factor(nr)1190 0.119
(0.176)
factor(nr)1204 0.888***
(0.180)
factor(nr)1249 0.468***
(0.180)
factor(nr)1272 0.612***
(0.176)
factor(nr)1311 0.481***
(0.176)
factor(nr)1316 0.921***
(0.178)
factor(nr)1318 0.625***
(0.192)
factor(nr)1345 0.549***
(0.178)
factor(nr)1397 0.653***
(0.180)
factor(nr)1434 -0.082
(0.177)
factor(nr)1492 0.408**
(0.178)
factor(nr)1496 -0.219
(0.176)
factor(nr)1506 0.082
(0.176)
factor(nr)1515 0.281
(0.176)
factor(nr)1520 0.375**
(0.181)
factor(nr)1528 0.136
(0.177)
factor(nr)1554 0.312*
(0.176)
factor(nr)1575 0.577***
(0.177)
factor(nr)1576 0.504***
(0.176)
factor(nr)1628 0.440**
(0.176)
factor(nr)1641 0.974***
(0.178)
factor(nr)1644 0.263
(0.176)
factor(nr)1653 0.629***
(0.176)
factor(nr)1654 0.663***
(0.178)
factor(nr)1721 1.160***
(0.179)
factor(nr)1742 0.861***
(0.176)
factor(nr)1744 0.557***
(0.176)
factor(nr)1763 -0.194
(0.176)
factor(nr)1777 0.115
(0.176)
factor(nr)1843 1.310***
(0.177)
factor(nr)1891 -0.090
(0.176)
factor(nr)1895 0.604***
(0.177)
factor(nr)1899 0.171
(0.177)
factor(nr)1925 0.488***
(0.176)
factor(nr)1930 0.251
(0.176)
factor(nr)1961 0.745***
(0.179)
factor(nr)1963 0.470***
(0.176)
factor(nr)1979 0.828***
(0.179)
factor(nr)1988 -0.062
(0.176)
factor(nr)2000 0.637***
(0.177)
factor(nr)2014 0.310*
(0.176)
factor(nr)2025 0.432**
(0.176)
factor(nr)2038 0.180
(0.176)
factor(nr)2075 0.928***
(0.181)
factor(nr)2101 1.158***
(0.176)
factor(nr)2106 0.595***
(0.179)
factor(nr)2107 0.460***
(0.176)
factor(nr)2108 0.816***
(0.177)
factor(nr)2147 -0.860***
(0.176)
factor(nr)2157 0.055
(0.180)
factor(nr)2163 1.092***
(0.179)
factor(nr)2173 0.148
(0.176)
factor(nr)2180 0.411**
(0.176)
factor(nr)2183 0.392**
(0.176)
factor(nr)2216 0.540***
(0.176)
factor(nr)2220 0.991***
(0.176)
factor(nr)2227 0.255
(0.177)
factor(nr)2264 -0.093
(0.176)
factor(nr)2306 -0.052
(0.177)
factor(nr)2312 0.816***
(0.176)
factor(nr)2314 0.969***
(0.180)
factor(nr)2329 0.545***
(0.176)
factor(nr)2335 0.506***
(0.179)
factor(nr)2341 0.471***
(0.176)
factor(nr)2351 0.046
(0.176)
factor(nr)2386 -0.154
(0.176)
factor(nr)2401 0.644***
(0.180)
factor(nr)2413 0.999***
(0.179)
factor(nr)2421 0.036
(0.177)
factor(nr)2445 0.463***
(0.178)
factor(nr)2451 0.592***
(0.177)
factor(nr)2494 0.168
(0.179)
factor(nr)2508 0.848***
(0.177)
factor(nr)2535 0.486***
(0.179)
factor(nr)2540 -0.059
(0.176)
factor(nr)2685 1.031***
(0.176)
factor(nr)2711 0.052
(0.176)
factor(nr)2718 1.059***
(0.177)
factor(nr)2721 0.157
(0.184)
factor(nr)2733 -0.146
(0.178)
factor(nr)2741 0.419**
(0.181)
factor(nr)2745 0.556***
(0.176)
factor(nr)2751 0.456**
(0.179)
factor(nr)2774 0.903***
(0.177)
factor(nr)2801 0.050
(0.176)
factor(nr)2813 0.222
(0.177)
factor(nr)2833 0.621***
(0.177)
factor(nr)2839 0.646***
(0.176)
factor(nr)2842 0.942***
(0.177)
factor(nr)2866 0.707***
(0.177)
factor(nr)2868 0.978***
(0.177)
factor(nr)2874 0.007
(0.177)
factor(nr)2916 0.345**
(0.176)
factor(nr)2951 0.313*
(0.182)
factor(nr)2980 0.327*
(0.177)
factor(nr)2994 0.506***
(0.177)
factor(nr)2997 0.601***
(0.176)
factor(nr)3017 0.936***
(0.176)
factor(nr)3037 1.040***
(0.179)
factor(nr)3059 0.694***
(0.181)
factor(nr)3062 1.166***
(0.176)
factor(nr)3100 0.637***
(0.179)
factor(nr)3102 -0.259
(0.176)
factor(nr)3127 -0.407**
(0.176)
factor(nr)3136 0.698***
(0.177)
factor(nr)3137 0.892***
(0.176)
factor(nr)3138 0.665***
(0.178)
factor(nr)3140 0.843***
(0.177)
factor(nr)3193 0.686***
(0.176)
factor(nr)3196 0.681***
(0.177)
factor(nr)3200 0.771***
(0.187)
factor(nr)3202 0.593***
(0.178)
factor(nr)3207 0.471***
(0.179)
factor(nr)3208 0.855***
(0.177)
factor(nr)3210 0.708***
(0.176)
factor(nr)3215 0.324*
(0.178)
factor(nr)3219 0.237
(0.176)
factor(nr)3226 0.642***
(0.176)
factor(nr)3235 0.144
(0.176)
factor(nr)3239 -0.375**
(0.175)
factor(nr)3271 0.756***
(0.182)
factor(nr)3275 0.542***
(0.176)
factor(nr)3282 0.660***
(0.176)
factor(nr)3289 0.454***
(0.176)
factor(nr)3290 0.456***
(0.176)
factor(nr)3307 1.321***
(0.177)
factor(nr)3333 -0.078
(0.176)
factor(nr)3353 0.083
(0.176)
factor(nr)3380 0.522***
(0.176)
factor(nr)3381 0.587***
(0.176)
factor(nr)3389 0.672***
(0.177)
factor(nr)3394 0.656***
(0.176)
factor(nr)3401 0.397**
(0.176)
factor(nr)3414 0.701***
(0.176)
factor(nr)3420 0.301*
(0.176)
factor(nr)3440 -0.211
(0.176)
factor(nr)3461 0.711***
(0.176)
factor(nr)3468 0.195
(0.176)
factor(nr)3482 1.056***
(0.176)
factor(nr)3495 0.538***
(0.180)
factor(nr)3503 0.965***
(0.178)
factor(nr)3525 1.040***
(0.175)
factor(nr)3526 0.594***
(0.178)
factor(nr)3538 0.962***
(0.181)
factor(nr)3563 0.636***
(0.177)
factor(nr)3575 0.997***
(0.178)
factor(nr)3580 0.361**
(0.176)
factor(nr)3581 0.671***
(0.176)
factor(nr)3589 0.287
(0.177)
factor(nr)3591 0.674***
(0.176)
factor(nr)3598 0.864***
(0.176)
factor(nr)3602 1.082***
(0.180)
factor(nr)3607 -0.019
(0.187)
factor(nr)3621 0.528***
(0.178)
factor(nr)3628 0.984***
(0.177)
factor(nr)3653 0.723***
(0.176)
factor(nr)3706 0.650***
(0.177)
factor(nr)3707 0.556***
(0.176)
factor(nr)3708 0.617***
(0.176)
factor(nr)3743 0.607***
(0.176)
factor(nr)3777 0.732***
(0.177)
factor(nr)3831 0.227
(0.176)
factor(nr)3844 0.510***
(0.176)
factor(nr)3847 1.104***
(0.178)
factor(nr)3848 0.651***
(0.176)
factor(nr)3882 0.047
(0.175)
factor(nr)3937 0.520***
(0.177)
factor(nr)4000 1.072***
(0.201)
factor(nr)4004 0.976***
(0.177)
factor(nr)4025 0.135
(0.176)
factor(nr)4032 0.157
(0.176)
factor(nr)4046 0.564***
(0.184)
factor(nr)4088 1.447***
(0.177)
factor(nr)4091 1.271***
(0.178)
factor(nr)4122 0.713***
(0.177)
factor(nr)4127 0.093
(0.176)
factor(nr)4128 0.297*
(0.178)
factor(nr)4159 0.605***
(0.176)
factor(nr)4204 0.324*
(0.177)
factor(nr)4229 0.314*
(0.176)
factor(nr)4258 0.718***
(0.176)
factor(nr)4261 1.342***
(0.200)
factor(nr)4264 0.073
(0.178)
factor(nr)4278 0.594***
(0.177)
factor(nr)4297 0.538***
(0.176)
factor(nr)4302 -0.129
(0.176)
factor(nr)4321 0.473***
(0.176)
factor(nr)4328 0.239
(0.177)
factor(nr)4332 -0.371**
(0.176)
factor(nr)4335 0.342*
(0.177)
factor(nr)4357 0.527***
(0.177)
factor(nr)4365 -0.039
(0.176)
factor(nr)4380 0.880***
(0.178)
factor(nr)4394 0.724***
(0.176)
factor(nr)4510 0.643***
(0.176)
factor(nr)4559 0.374**
(0.180)
factor(nr)4563 0.019
(0.176)
factor(nr)4569 0.791***
(0.176)
factor(nr)4603 0.734***
(0.176)
factor(nr)4607 0.166
(0.176)
factor(nr)4633 0.505***
(0.176)
factor(nr)4676 0.125
(0.176)
factor(nr)4701 0.952***
(0.176)
factor(nr)4716 0.122
(0.178)
factor(nr)4720 1.137***
(0.181)
factor(nr)4759 0.596***
(0.179)
factor(nr)4791 0.678***
(0.181)
factor(nr)4811 0.096
(0.176)
factor(nr)4828 0.108
(0.176)
factor(nr)4857 -0.098
(0.176)
factor(nr)4858 0.976***
(0.176)
factor(nr)4859 0.031
(0.176)
factor(nr)4866 0.818***
(0.177)
factor(nr)4881 0.358**
(0.177)
factor(nr)4884 0.522***
(0.178)
factor(nr)4888 0.096
(0.177)
factor(nr)4901 0.218
(0.179)
factor(nr)4917 0.059
(0.177)
factor(nr)4926 0.440**
(0.178)
factor(nr)4982 0.102
(0.178)
factor(nr)5017 1.088***
(0.176)
factor(nr)5033 1.061***
(0.176)
factor(nr)5048 0.315*
(0.176)
factor(nr)5122 0.657***
(0.177)
factor(nr)5141 0.711***
(0.177)
factor(nr)5147 1.045***
(0.179)
factor(nr)5158 0.700***
(0.176)
factor(nr)5221 0.538***
(0.177)
factor(nr)5223 0.486***
(0.176)
factor(nr)5227 0.652***
(0.179)
factor(nr)5248 0.179
(0.176)
factor(nr)5252 0.088
(0.176)
factor(nr)5263 0.494***
(0.177)
factor(nr)5274 0.756***
(0.176)
factor(nr)5335 0.318*
(0.177)
factor(nr)5345 0.233
(0.176)
factor(nr)5359 -0.082
(0.177)
factor(nr)5368 0.060
(0.176)
factor(nr)5377 0.382**
(0.176)
factor(nr)5390 0.288
(0.177)
factor(nr)5419 0.125
(0.176)
factor(nr)5435 0.033
(0.176)
factor(nr)5437 0.265
(0.177)
factor(nr)5497 0.195
(0.177)
factor(nr)5525 0.315*
(0.180)
factor(nr)5529 0.573***
(0.179)
factor(nr)5531 0.927***
(0.180)
factor(nr)5579 0.229
(0.176)
factor(nr)5588 0.936***
(0.194)
factor(nr)5599 0.569***
(0.176)
factor(nr)5650 0.330*
(0.176)
factor(nr)5660 0.724***
(0.176)
factor(nr)5665 0.155
(0.176)
factor(nr)5666 0.495***
(0.176)
factor(nr)5698 0.686***
(0.179)
factor(nr)5699 0.679***
(0.176)
factor(nr)5731 0.318*
(0.177)
factor(nr)5750 0.661***
(0.181)
factor(nr)5755 0.546***
(0.179)
factor(nr)5772 0.126
(0.179)
factor(nr)5816 0.211
(0.177)
factor(nr)5823 0.107
(0.176)
factor(nr)5851 0.061
(0.176)
factor(nr)5857 0.438**
(0.176)
factor(nr)5859 0.427**
(0.177)
factor(nr)6016 0.794***
(0.176)
factor(nr)6020 -0.282
(0.177)
factor(nr)6025 -0.425**
(0.177)
factor(nr)6056 -0.104
(0.176)
factor(nr)6094 0.484***
(0.178)
factor(nr)6186 0.487***
(0.176)
factor(nr)6395 0.979***
(0.188)
factor(nr)6430 0.403**
(0.180)
factor(nr)6446 0.555***
(0.177)
factor(nr)6463 0.352*
(0.187)
factor(nr)6558 0.807***
(0.176)
factor(nr)6559 0.581***
(0.176)
factor(nr)6561 0.953***
(0.176)
factor(nr)6574 0.098
(0.178)
factor(nr)6648 0.774***
(0.176)
factor(nr)6813 0.274
(0.177)
factor(nr)6824 0.419**
(0.179)
factor(nr)6888 0.494***
(0.187)
factor(nr)6942 0.549***
(0.176)
factor(nr)6954 0.565***
(0.177)
factor(nr)6955 0.678***
(0.176)
factor(nr)6964 0.473***
(0.179)
factor(nr)6987 1.456***
(0.176)
factor(nr)7025 0.906***
(0.179)
factor(nr)7043 0.498***
(0.176)
factor(nr)7060 0.460***
(0.176)
factor(nr)7087 -0.207
(0.176)
factor(nr)7238 0.680***
(0.193)
factor(nr)7279 0.270
(0.178)
factor(nr)7342 0.432**
(0.179)
factor(nr)7343 0.350**
(0.176)
factor(nr)7411 -0.038
(0.176)
factor(nr)7424 0.651***
(0.176)
factor(nr)7429 0.515***
(0.182)
factor(nr)7454 0.730***
(0.176)
factor(nr)7472 0.402**
(0.177)
factor(nr)7474 0.303*
(0.176)
factor(nr)7509 0.689***
(0.181)
factor(nr)7539 -0.012
(0.176)
factor(nr)7769 0.655***
(0.177)
factor(nr)7783 0.449**
(0.176)
factor(nr)7784 1.929***
(0.176)
factor(nr)7801 -0.048
(0.176)
factor(nr)7824 0.546***
(0.176)
factor(nr)7874 1.107***
(0.176)
factor(nr)7887 0.639***
(0.178)
factor(nr)7923 1.238***
(0.180)
factor(nr)7926 0.708***
(0.181)
factor(nr)8021 0.824***
(0.176)
factor(nr)8087 0.460***
(0.176)
factor(nr)8089 0.222
(0.177)
factor(nr)8090 1.226***
(0.176)
factor(nr)8096 1.299***
(0.221)
factor(nr)8106 0.948***
(0.200)
factor(nr)8107 1.186***
(0.221)
factor(nr)8142 0.182
(0.176)
factor(nr)8168 0.551***
(0.177)
factor(nr)8173 0.909***
(0.202)
factor(nr)8203 1.072***
(0.177)
factor(nr)8211 0.294
(0.183)
factor(nr)8224 0.807***
(0.179)
factor(nr)8272 0.959***
(0.178)
factor(nr)8300 0.386**
(0.176)
factor(nr)8304 0.470***
(0.176)
factor(nr)8364 0.348**
(0.177)
factor(nr)8370 0.845***
(0.177)
factor(nr)8381 0.218
(0.176)
factor(nr)8388 0.743***
(0.194)
factor(nr)8406 0.626***
(0.184)
factor(nr)8415 0.054
(0.176)
factor(nr)8496 -0.112
(0.176)
factor(nr)8501 -0.070
(0.179)
factor(nr)8518 1.243***
(0.180)
factor(nr)8520 -0.353**
(0.176)
factor(nr)8524 -0.118
(0.177)
factor(nr)8548 0.115
(0.176)
factor(nr)8556 0.625***
(0.176)
factor(nr)8564 0.106
(0.176)
factor(nr)8581 -0.249
(0.176)
factor(nr)8586 0.258
(0.176)
factor(nr)8587 -0.370**
(0.176)
factor(nr)8597 0.771***
(0.183)
factor(nr)8656 0.153
(0.176)
factor(nr)8722 0.637***
(0.177)
factor(nr)8743 0.515***
(0.177)
factor(nr)8749 0.940***
(0.202)
factor(nr)8758 0.535***
(0.177)
factor(nr)8796 0.780***
(0.176)
factor(nr)8838 0.406**
(0.176)
factor(nr)8842 0.145
(0.176)
factor(nr)8846 0.112
(0.177)
factor(nr)8860 0.124
(0.178)
factor(nr)8862 0.399**
(0.176)
factor(nr)8880 1.219***
(0.178)
factor(nr)8886 0.631***
(0.179)
factor(nr)8903 -0.239
(0.176)
factor(nr)8908 -0.023
(0.177)
factor(nr)8911 -0.034
(0.177)
factor(nr)8917 0.796***
(0.178)
factor(nr)8991 0.913***
(0.176)
factor(nr)8997 0.898***
(0.176)
factor(nr)9014 0.540***
(0.177)
factor(nr)9015 0.697***
(0.187)
factor(nr)9027 1.002***
(0.176)
factor(nr)9066 -0.153
(0.176)
factor(nr)9082 0.274
(0.178)
factor(nr)9131 0.758***
(0.201)
factor(nr)9132 0.709***
(0.188)
factor(nr)9154 1.113***
(0.176)
factor(nr)9158 0.086
(0.179)
factor(nr)9184 0.164
(0.177)
factor(nr)9230 0.158
(0.176)
factor(nr)9265 0.437**
(0.175)
factor(nr)9367 0.207
(0.176)
factor(nr)9390 0.745***
(0.177)
factor(nr)9391 0.370**
(0.176)
factor(nr)9418 1.133***
(0.176)
factor(nr)9424 0.806***
(0.177)
factor(nr)9447 0.503***
(0.176)
factor(nr)9449 0.318*
(0.176)
factor(nr)9453 0.745***
(0.176)
factor(nr)9468 0.493***
(0.176)
factor(nr)9502 0.895***
(0.181)
factor(nr)9505 0.046
(0.179)
factor(nr)9603 0.310*
(0.188)
factor(nr)9643 0.433**
(0.176)
factor(nr)9667 1.067***
(0.176)
factor(nr)9683 0.128
(0.180)
factor(nr)9694 0.847***
(0.176)
factor(nr)9710 0.280
(0.177)
factor(nr)9718 0.938***
(0.176)
factor(nr)9725 0.322*
(0.176)
factor(nr)9744 0.689***
(0.176)
factor(nr)9752 1.390***
(0.176)
factor(nr)9776 0.953***
(0.178)
factor(nr)9786 0.624***
(0.176)
factor(nr)9791 0.328*
(0.176)
factor(nr)9794 0.473***
(0.177)
factor(nr)9810 -0.144
(0.176)
factor(nr)9846 0.825***
(0.177)
factor(nr)9859 0.148
(0.178)
factor(nr)9868 0.029
(0.176)
factor(nr)9876 0.853***
(0.179)
factor(nr)9883 0.714***
(0.176)
factor(nr)9889 0.988***
(0.177)
factor(nr)9901 0.689***
(0.177)
factor(nr)9936 0.895***
(0.177)
factor(nr)9964 0.412**
(0.177)
factor(nr)10043 -0.172
(0.178)
factor(nr)10067 0.510***
(0.176)
factor(nr)10091 0.697***
(0.181)
factor(nr)10120 -0.118
(0.176)
factor(nr)10121 0.325*
(0.176)
factor(nr)10167 0.567***
(0.178)
factor(nr)10209 0.112
(0.176)
factor(nr)10230 0.724***
(0.180)
factor(nr)10265 0.993***
(0.176)
factor(nr)10274 0.237
(0.176)
factor(nr)10311 0.301*
(0.176)
factor(nr)10392 0.108
(0.177)
factor(nr)10425 0.945***
(0.177)
factor(nr)10441 0.176
(0.176)
factor(nr)10457 0.446**
(0.176)
factor(nr)10469 0.447**
(0.176)
factor(nr)10524 0.088
(0.177)
factor(nr)10552 -0.185
(0.176)
factor(nr)10553 0.706***
(0.179)
factor(nr)10570 -0.747***
(0.177)
factor(nr)10593 0.284
(0.184)
factor(nr)10666 -0.324*
(0.177)
factor(nr)11275 0.146
(0.176)
factor(nr)11328 0.495***
(0.179)
factor(nr)11750 0.384**
(0.176)
factor(nr)11821 0.808***
(0.176)
factor(nr)11857 0.934***
(0.177)
factor(nr)11887 0.396**
(0.176)
factor(nr)11890 1.093***
(0.211)
factor(nr)11892 1.132***
(0.177)
factor(nr)11924 0.354**
(0.176)
factor(nr)11925 0.408**
(0.176)
factor(nr)11957 0.004
(0.177)
factor(nr)11973 0.578***
(0.177)
factor(nr)11990 1.010***
(0.176)
factor(nr)12012 0.224
(0.176)
factor(nr)12013 0.568***
(0.176)
factor(nr)12045 0.200
(0.176)
factor(nr)12055 0.674***
(0.177)
factor(nr)12084 0.450**
(0.179)
factor(nr)12088 0.117
(0.176)
factor(nr)12122 0.586***
(0.202)
factor(nr)12179 0.301*
(0.177)
factor(nr)12182 0.515***
(0.176)
factor(nr)12220 0.673***
(0.177)
factor(nr)12221 -0.121
(0.183)
factor(nr)12245 -0.110
(0.176)
factor(nr)12276 0.655***
(0.177)
factor(nr)12385 0.819***
(0.179)
factor(nr)12410 0.040
(0.178)
factor(nr)12420 0.840***
(0.177)
factor(nr)12433 0.393**
(0.176)
factor(nr)12451 0.431**
(0.176)
factor(nr)12477 1.004***
(0.179)
factor(nr)12500 0.222
(0.178)
factor(nr)12534 0.942***
(0.176)
factor(nr)12548 0.347*
(0.180)
educ
black
hisp
exper
Constant -0.445*** 0.933***
(0.030) (0.125)
--------------------------------------------------------------------------------------------------
Observations 4,360 4,360 4,360
R2 0.181 0.181 0.621
Adjusted R2 0.179 0.061 0.566
Residual Std. Error 0.328 (df = 4349) 0.351 (df = 3805)
F Statistic 95.840*** (df = 10; 4349) 83.851*** (df = 10; 3805) 11.250*** (df = 554; 3805)
==================================================================================================
Note: *p<0.1; **p<0.05; ***p<0.01Stata
use "files/WAGEPAN.dta" , clear
bys nr: egen lwage_mean = mean(lwage)
bys nr: egen expersq_mean = mean(expersq)
bys nr: egen married_mean = mean(married)
bys nr: egen union_mean = mean(union)
gen lwage_demean = lwage - lwage_mean
gen expersq_demean = expersq - expersq_mean
gen married_demean = married - married_mean
gen union_demean = union - union_mean
xtset nr year
eststo: qui reg lwage_demean expersq_demean married_demean union_demean i.year
eststo: qui xtreg lwage expersq married union i.year educ black hisp exper , fe
eststo: qui reg lwage expersq married union i.year i.nr educ black hisp exper
esttab , mtitles("Demean" "FE" "LSDV") compressPanel variable: nr (strongly balanced)
Time variable: year, 1980 to 1987
Delta: 1 unit
(est1 stored)
(est2 stored)
(est3 stored)
-------------------------------------------------
(1) (2) (3)
Demean FE LSDV
-------------------------------------------------
expe~emean -0.00519***
(-7.87)
marr~emean 0.0467**
(2.73)
union_de~n 0.0800***
(4.43)
1980.year 0 0 0
(.) (.) (.)
1981.year 0.151*** 0.151*** 0.151***
(7.36) (6.89) (6.89)
1982.year 0.253*** 0.253*** 0.253***
(11.08) (10.36) (10.36)
1983.year 0.354*** 0.354*** 0.354***
(12.96) (12.12) (12.12)
1984.year 0.490*** 0.490*** 0.490***
(14.46) (13.53) (13.53)
1985.year 0.617*** 0.617*** 0.617***
(14.59) (13.65) (13.65)
1986.year 0.765*** 0.765*** 0.765***
(14.58) (13.64) (13.64)
1987.year 0.925*** 0.925*** 0.925***
(14.38) (13.45) (13.45)
expersq -0.00519*** -0.00519***
(-7.36) (-7.36)
married 0.0467* 0.0467*
(2.55) (2.55)
union 0.0800*** 0.0800***
(4.14) (4.14)
educ 0 0
(.) (.)
black 0 0
(.) (.)
hisp 0 0
(.) (.)
exper 0 0
(.) (.)
13.nr 0
(.)
17.nr 0.579**
(3.26)
18.nr 0.929***
(5.20)
45.nr 0.554**
(3.15)
110.nr 1.046***
(5.82)
120.nr 0.239
(1.36)
126.nr 0.783***
(4.45)
150.nr -0.140
(-0.80)
162.nr 0.269
(1.53)
166.nr 0.138
(0.78)
189.nr 0.191
(1.09)
193.nr 0.981***
(5.58)
209.nr 0.707***
(4.01)
212.nr 0.833***
(4.74)
218.nr 1.231***
(6.99)
243.nr 0.586***
(3.29)
259.nr 0.478**
(2.69)
260.nr 0.789***
(4.48)
309.nr 1.052***
(5.95)
351.nr 0.358*
(2.02)
353.nr 0.583***
(3.31)
383.nr 0.564**
(3.21)
408.nr 0.801***
(4.54)
424.nr 1.345***
(7.45)
464.nr 0.0803
(0.46)
483.nr 0.713***
(3.98)
556.nr 1.089***
(6.20)
560.nr 0.205
(1.17)
569.nr -0.431*
(-2.45)
583.nr 0.852***
(4.80)
647.nr 0.360*
(2.04)
658.nr 0.838***
(4.73)
684.nr 1.132***
(6.42)
711.nr -0.0972
(-0.55)
729.nr 0.837***
(4.74)
731.nr 0.574**
(3.23)
732.nr 0.531**
(3.02)
793.nr 0.498**
(2.84)
797.nr 0.841***
(4.75)
800.nr 0.380*
(2.15)
813.nr -0.657***
(-3.74)
823.nr -0.393*
(-2.23)
827.nr 0.507**
(2.88)
847.nr 0.489**
(2.79)
851.nr 0.735***
(4.17)
863.nr 0.550**
(3.13)
873.nr -0.127
(-0.72)
891.nr 0.735***
(4.16)
908.nr -0.405*
(-2.30)
910.nr 0.679***
(3.87)
916.nr 0.564**
(3.21)
919.nr 0.238
(1.34)
922.nr 1.011***
(5.76)
924.nr -0.0709
(-0.40)
925.nr 0.809***
(4.60)
944.nr 0.106
(0.60)
945.nr 0.106
(0.60)
947.nr 1.154***
(6.52)
955.nr 1.006***
(5.64)
965.nr 0.434*
(2.42)
996.nr 0.00740
(0.04)
1007.nr 0.996***
(5.61)
1054.nr 0.133
(0.75)
1064.nr 0.858***
(4.81)
1081.nr 0.179
(1.02)
1085.nr 0.114
(0.65)
1091.nr 0.226
(1.23)
1094.nr 0.600***
(3.38)
1096.nr 0.251
(1.37)
1098.nr 0.837***
(4.77)
1102.nr 0.948***
(5.38)
1107.nr 0.762***
(4.23)
1142.nr 0.715***
(4.07)
1156.nr 0.569**
(3.17)
1180.nr 0.636***
(3.61)
1190.nr 0.119
(0.68)
1204.nr 0.888***
(4.93)
1249.nr 0.468**
(2.60)
1272.nr 0.612***
(3.47)
1311.nr 0.481**
(2.74)
1316.nr 0.921***
(5.17)
1318.nr 0.625**
(3.25)
1345.nr 0.549**
(3.08)
1397.nr 0.653***
(3.62)
1434.nr -0.0818
(-0.46)
1492.nr 0.408*
(2.30)
1496.nr -0.219
(-1.24)
1506.nr 0.0822
(0.47)
1515.nr 0.281
(1.60)
1520.nr 0.375*
(2.07)
1528.nr 0.136
(0.77)
1554.nr 0.312
(1.77)
1575.nr 0.577**
(3.26)
1576.nr 0.504**
(2.86)
1628.nr 0.440*
(2.50)
1641.nr 0.974***
(5.46)
1644.nr 0.263
(1.50)
1653.nr 0.629***
(3.58)
1654.nr 0.663***
(3.73)
1721.nr 1.160***
(6.47)
1742.nr 0.861***
(4.90)
1744.nr 0.557**
(3.16)
1763.nr -0.194
(-1.11)
1777.nr 0.115
(0.65)
1843.nr 1.310***
(7.41)
1891.nr -0.0896
(-0.51)
1895.nr 0.604***
(3.41)
1899.nr 0.171
(0.97)
1925.nr 0.488**
(2.78)
1930.nr 0.251
(1.43)
1961.nr 0.745***
(4.18)
1963.nr 0.470**
(2.66)
1979.nr 0.828***
(4.63)
1988.nr -0.0621
(-0.35)
2000.nr 0.637***
(3.60)
2014.nr 0.310
(1.77)
2025.nr 0.432*
(2.45)
2038.nr 0.180
(1.02)
2075.nr 0.928***
(5.14)
2101.nr 1.158***
(6.57)
2106.nr 0.595***
(3.33)
2107.nr 0.460**
(2.62)
2108.nr 0.816***
(4.61)
2147.nr -0.860***
(-4.90)
2157.nr 0.0546
(0.30)
2163.nr 1.092***
(6.09)
2173.nr 0.148
(0.84)
2180.nr 0.411*
(2.34)
2183.nr 0.392*
(2.23)
2216.nr 0.540**
(3.07)
2220.nr 0.991***
(5.63)
2227.nr 0.255
(1.44)
2264.nr -0.0930
(-0.53)
2306.nr -0.0521
(-0.29)
2312.nr 0.816***
(4.64)
2314.nr 0.969***
(5.39)
2329.nr 0.545**
(3.09)
2335.nr 0.506**
(2.82)
2341.nr 0.471**
(2.68)
2351.nr 0.0458
(0.26)
2386.nr -0.154
(-0.87)
2401.nr 0.644***
(3.57)
2413.nr 0.999***
(5.59)
2421.nr 0.0360
(0.20)
2445.nr 0.463**
(2.60)
2451.nr 0.592***
(3.35)
2494.nr 0.168
(0.94)
2508.nr 0.848***
(4.79)
2535.nr 0.486**
(2.72)
2540.nr -0.0591
(-0.34)
2685.nr 1.031***
(5.87)
2711.nr 0.0516
(0.29)
2718.nr 1.059***
(5.98)
2721.nr 0.157
(0.86)
2733.nr -0.146
(-0.82)
2741.nr 0.419*
(2.32)
2745.nr 0.556**
(3.15)
2751.nr 0.456*
(2.55)
2774.nr 0.903***
(5.09)
2801.nr 0.0497
(0.28)
2813.nr 0.222
(1.26)
2833.nr 0.621***
(3.52)
2839.nr 0.646***
(3.66)
2842.nr 0.942***
(5.31)
2866.nr 0.707***
(3.99)
2868.nr 0.978***
(5.54)
2874.nr 0.00693
(0.04)
2916.nr 0.345*
(1.96)
2951.nr 0.313
(1.71)
2980.nr 0.327
(1.85)
2994.nr 0.506**
(2.86)
2997.nr 0.601***
(3.41)
3017.nr 0.936***
(5.31)
3037.nr 1.040***
(5.81)
3059.nr 0.694***
(3.84)
3062.nr 1.166***
(6.64)
3100.nr 0.637***
(3.57)
3102.nr -0.259
(-1.48)
3127.nr -0.407*
(-2.31)
3136.nr 0.698***
(3.94)
3137.nr 0.892***
(5.08)
3138.nr 0.665***
(3.75)
3140.nr 0.843***
(4.77)
3193.nr 0.686***
(3.90)
3196.nr 0.681***
(3.85)
3200.nr 0.771***
(4.12)
3202.nr 0.593***
(3.34)
3207.nr 0.471**
(2.64)
3208.nr 0.855***
(4.82)
3210.nr 0.708***
(4.02)
3215.nr 0.324
(1.82)
3219.nr 0.237
(1.35)
3226.nr 0.642***
(3.64)
3235.nr 0.144
(0.81)
3239.nr -0.375*
(-2.14)
3271.nr 0.756***
(4.15)
3275.nr 0.542**
(3.09)
3282.nr 0.660***
(3.75)
3289.nr 0.454**
(2.58)
3290.nr 0.456**
(2.60)
3307.nr 1.321***
(7.47)
3333.nr -0.0781
(-0.44)
3353.nr 0.0825
(0.47)
3380.nr 0.522**
(2.96)
3381.nr 0.587***
(3.34)
3389.nr 0.672***
(3.81)
3394.nr 0.656***
(3.73)
3401.nr 0.397*
(2.25)
3414.nr 0.701***
(3.99)
3420.nr 0.301
(1.71)
3440.nr -0.211
(-1.20)
3461.nr 0.711***
(4.05)
3468.nr 0.195
(1.11)
3482.nr 1.056***
(5.99)
3495.nr 0.538**
(2.99)
3503.nr 0.965***
(5.42)
3525.nr 1.040***
(5.93)
3526.nr 0.594***
(3.33)
3538.nr 0.962***
(5.33)
3563.nr 0.636***
(3.60)
3575.nr 0.997***
(5.59)
3580.nr 0.361*
(2.06)
3581.nr 0.671***
(3.82)
3589.nr 0.287
(1.62)
3591.nr 0.674***
(3.82)
3598.nr 0.864***
(4.90)
3602.nr 1.082***
(6.00)
3607.nr -0.0189
(-0.10)
3621.nr 0.528**
(2.97)
3628.nr 0.984***
(5.55)
3653.nr 0.723***
(4.10)
3706.nr 0.650***
(3.67)
3707.nr 0.556**
(3.15)
3708.nr 0.617***
(3.51)
3743.nr 0.607***
(3.45)
3777.nr 0.732***
(4.13)
3831.nr 0.227
(1.29)
3844.nr 0.510**
(2.89)
3847.nr 1.104***
(6.22)
3848.nr 0.651***
(3.71)
3882.nr 0.0468
(0.27)
3937.nr 0.520**
(2.94)
4000.nr 1.072***
(5.34)
4004.nr 0.976***
(5.50)
4025.nr 0.135
(0.77)
4032.nr 0.157
(0.89)
4046.nr 0.564**
(3.07)
4088.nr 1.447***
(8.16)
4091.nr 1.271***
(7.14)
4122.nr 0.713***
(4.04)
4127.nr 0.0934
(0.53)
4128.nr 0.297
(1.67)
4159.nr 0.605***
(3.43)
4204.nr 0.324
(1.82)
4229.nr 0.314
(1.79)
4258.nr 0.718***
(4.07)
4261.nr 1.342***
(6.70)
4264.nr 0.0729
(0.41)
4278.nr 0.594***
(3.35)
4297.nr 0.538**
(3.05)
4302.nr -0.129
(-0.74)
4321.nr 0.473**
(2.68)
4328.nr 0.239
(1.35)
4332.nr -0.371*
(-2.11)
4335.nr 0.342
(1.93)
4357.nr 0.527**
(2.98)
4365.nr -0.0388
(-0.22)
4380.nr 0.880***
(4.94)
4394.nr 0.724***
(4.12)
4510.nr 0.643***
(3.66)
4559.nr 0.374*
(2.08)
4563.nr 0.0190
(0.11)
4569.nr 0.791***
(4.48)
4603.nr 0.734***
(4.16)
4607.nr 0.166
(0.94)
4633.nr 0.505**
(2.86)
4676.nr 0.125
(0.71)
4701.nr 0.952***
(5.42)
4716.nr 0.122
(0.69)
4720.nr 1.137***
(6.28)
4759.nr 0.596***
(3.33)
4791.nr 0.678***
(3.74)
4811.nr 0.0962
(0.55)
4828.nr 0.108
(0.61)
4857.nr -0.0984
(-0.56)
4858.nr 0.976***
(5.54)
4859.nr 0.0313
(0.18)
4866.nr 0.818***
(4.62)
4881.nr 0.358*
(2.02)
4884.nr 0.522**
(2.93)
4888.nr 0.0963
(0.55)
4901.nr 0.218
(1.22)
4917.nr 0.0595
(0.34)
4926.nr 0.440*
(2.47)
4982.nr 0.102
(0.57)
5017.nr 1.088***
(6.19)
5033.nr 1.061***
(6.03)
5048.nr 0.315
(1.79)
5122.nr 0.657***
(3.70)
5141.nr 0.711***
(4.03)
5147.nr 1.045***
(5.84)
5158.nr 0.700***
(3.97)
5221.nr 0.538**
(3.04)
5223.nr 0.486**
(2.76)
5227.nr 0.652***
(3.63)
5248.nr 0.179
(1.02)
5252.nr 0.0879
(0.50)
5263.nr 0.494**
(2.79)
5274.nr 0.756***
(4.28)
5335.nr 0.318
(1.80)
5345.nr 0.233
(1.33)
5359.nr -0.0821
(-0.46)
5368.nr 0.0598
(0.34)
5377.nr 0.382*
(2.18)
5390.nr 0.288
(1.63)
5419.nr 0.125
(0.71)
5435.nr 0.0333
(0.19)
5437.nr 0.265
(1.50)
5497.nr 0.195
(1.10)
5525.nr 0.315
(1.75)
5529.nr 0.573**
(3.21)
5531.nr 0.927***
(5.16)
5579.nr 0.229
(1.30)
5588.nr 0.936***
(4.83)
5599.nr 0.569**
(3.23)
5650.nr 0.330
(1.87)
5660.nr 0.724***
(4.11)
5665.nr 0.155
(0.88)
5666.nr 0.495**
(2.81)
5698.nr 0.686***
(3.84)
5699.nr 0.679***
(3.85)
5731.nr 0.318
(1.80)
5750.nr 0.661***
(3.66)
5755.nr 0.546**
(3.06)
5772.nr 0.126
(0.71)
5816.nr 0.211
(1.19)
5823.nr 0.107
(0.61)
5851.nr 0.0606
(0.35)
5857.nr 0.438*
(2.49)
5859.nr 0.427*
(2.42)
6016.nr 0.794***
(4.52)
6020.nr -0.282
(-1.59)
6025.nr -0.425*
(-2.41)
6056.nr -0.104
(-0.59)
6094.nr 0.484**
(2.72)
6186.nr 0.487**
(2.76)
6395.nr 0.979***
(5.21)
6430.nr 0.403*
(2.24)
6446.nr 0.555**
(3.14)
6463.nr 0.352
(1.88)
6558.nr 0.807***
(4.58)
6559.nr 0.581**
(3.29)
6561.nr 0.953***
(5.42)
6574.nr 0.0977
(0.55)
6648.nr 0.774***
(4.40)
6813.nr 0.274
(1.55)
6824.nr 0.419*
(2.34)
6888.nr 0.494**
(2.64)
6942.nr 0.549**
(3.12)
6954.nr 0.565**
(3.20)
6955.nr 0.678***
(3.85)
6964.nr 0.473**
(2.64)
6987.nr 1.456***
(8.26)
7025.nr 0.906***
(5.07)
7043.nr 0.498**
(2.82)
7060.nr 0.460**
(2.61)
7087.nr -0.207
(-1.18)
7238.nr 0.680***
(3.52)
7279.nr 0.270
(1.51)
7342.nr 0.432*
(2.41)
7343.nr 0.350*
(1.99)
7411.nr -0.0378
(-0.21)
7424.nr 0.651***
(3.70)
7429.nr 0.515**
(2.83)
7454.nr 0.730***
(4.16)
7472.nr 0.402*
(2.27)
7474.nr 0.303
(1.72)
7509.nr 0.689***
(3.80)
7539.nr -0.0121
(-0.07)
7769.nr 0.655***
(3.71)
7783.nr 0.449*
(2.55)
7784.nr 1.929***
(10.99)
7801.nr -0.0478
(-0.27)
7824.nr 0.546**
(3.11)
7874.nr 1.107***
(6.30)
7887.nr 0.639***
(3.59)
7923.nr 1.238***
(6.88)
7926.nr 0.708***
(3.91)
8021.nr 0.824***
(4.69)
8087.nr 0.460**
(2.61)
8089.nr 0.222
(1.26)
8090.nr 1.226***
(6.97)
8096.nr 1.299***
(5.89)
8106.nr 0.948***
(4.74)
8107.nr 1.186***
(5.38)
8142.nr 0.182
(1.04)
8168.nr 0.551**
(3.12)
8173.nr 0.909***
(4.51)
8203.nr 1.072***
(6.07)
8211.nr 0.294
(1.61)
8224.nr 0.807***
(4.50)
8272.nr 0.959***
(5.40)
8300.nr 0.386*
(2.20)
8304.nr 0.470**
(2.67)
8364.nr 0.348*
(1.96)
8370.nr 0.845***
(4.78)
8381.nr 0.218
(1.24)
8388.nr 0.743***
(3.83)
8406.nr 0.626***
(3.41)
8415.nr 0.0542
(0.31)
8496.nr -0.112
(-0.64)
8501.nr -0.0699
(-0.39)
8518.nr 1.243***
(6.89)
8520.nr -0.353*
(-2.00)
8524.nr -0.118
(-0.67)
8548.nr 0.115
(0.65)
8556.nr 0.625***
(3.55)
8564.nr 0.106
(0.60)
8581.nr -0.249
(-1.41)
8586.nr 0.258
(1.47)
8587.nr -0.370*
(-2.10)
8597.nr 0.771***
(4.21)
8656.nr 0.153
(0.87)
8722.nr 0.637***
(3.59)
8743.nr 0.515**
(2.90)
8749.nr 0.940***
(4.67)
8758.nr 0.535**
(3.02)
8796.nr 0.780***
(4.42)
8838.nr 0.406*
(2.30)
8842.nr 0.145
(0.82)
8846.nr 0.112
(0.63)
8860.nr 0.124
(0.70)
8862.nr 0.399*
(2.27)
8880.nr 1.219***
(6.85)
8886.nr 0.631***
(3.52)
8903.nr -0.239
(-1.35)
8908.nr -0.0227
(-0.13)
8911.nr -0.0340
(-0.19)
8917.nr 0.796***
(4.48)
8991.nr 0.913***
(5.18)
8997.nr 0.898***
(5.09)
9014.nr 0.540**
(3.05)
9015.nr 0.697***
(3.72)
9027.nr 1.002***
(5.68)
9066.nr -0.153
(-0.87)
9082.nr 0.274
(1.54)
9131.nr 0.758***
(3.77)
9132.nr 0.709***
(3.77)
9154.nr 1.113***
(6.32)
9158.nr 0.0857
(0.48)
9184.nr 0.164
(0.92)
9230.nr 0.158
(0.90)
9265.nr 0.437*
(2.49)
9367.nr 0.207
(1.18)
9390.nr 0.745***
(4.20)
9391.nr 0.370*
(2.10)
9418.nr 1.133***
(6.44)
9424.nr 0.806***
(4.56)
9447.nr 0.503**
(2.85)
9449.nr 0.318
(1.81)
9453.nr 0.745***
(4.22)
9468.nr 0.493**
(2.81)
9502.nr 0.895***
(4.95)
9505.nr 0.0464
(0.26)
9603.nr 0.310
(1.65)
9643.nr 0.433*
(2.46)
9667.nr 1.067***
(6.07)
9683.nr 0.128
(0.71)
9694.nr 0.847***
(4.82)
9710.nr 0.280
(1.58)
9718.nr 0.938***
(5.34)
9725.nr 0.322
(1.84)
9744.nr 0.689***
(3.92)
9752.nr 1.390***
(7.88)
9776.nr 0.953***
(5.37)
9786.nr 0.624***
(3.55)
9791.nr 0.328
(1.86)
9794.nr 0.473**
(2.67)
9810.nr -0.144
(-0.82)
9846.nr 0.825***
(4.65)
9859.nr 0.148
(0.83)
9868.nr 0.0289
(0.16)
9876.nr 0.853***
(4.78)
9883.nr 0.714***
(4.05)
9889.nr 0.988***
(5.59)
9901.nr 0.689***
(3.88)
9936.nr 0.895***
(5.06)
9964.nr 0.412*
(2.32)
10043.nr -0.172
(-0.97)
10067.nr 0.510**
(2.89)
10091.nr 0.697***
(3.86)
10120.nr -0.118
(-0.67)
10121.nr 0.325
(1.85)
10167.nr 0.567**
(3.18)
10209.nr 0.112
(0.63)
10230.nr 0.724***
(4.03)
10265.nr 0.993***
(5.63)
10274.nr 0.237
(1.35)
10311.nr 0.301
(1.71)
10392.nr 0.108
(0.61)
10425.nr 0.945***
(5.34)
10441.nr 0.176
(1.00)
10457.nr 0.446*
(2.53)
10469.nr 0.447*
(2.54)
10524.nr 0.0885
(0.50)
10552.nr -0.185
(-1.05)
10553.nr 0.706***
(3.96)
10570.nr -0.747***
(-4.23)
10593.nr 0.284
(1.54)
10666.nr -0.324
(-1.83)
11275.nr 0.146
(0.83)
11328.nr 0.495**
(2.76)
11750.nr 0.384*
(2.19)
11821.nr 0.808***
(4.60)
11857.nr 0.934***
(5.27)
11887.nr 0.396*
(2.24)
11890.nr 1.093***
(5.18)
11892.nr 1.132***
(6.38)
11924.nr 0.354*
(2.02)
11925.nr 0.408*
(2.31)
11957.nr 0.00425
(0.02)
11973.nr 0.578**
(3.26)
11990.nr 1.010***
(5.73)
12012.nr 0.224
(1.27)
12013.nr 0.568**
(3.24)
12045.nr 0.200
(1.13)
12055.nr 0.674***
(3.81)
12084.nr 0.450*
(2.51)
12088.nr 0.117
(0.66)
12122.nr 0.586**
(2.91)
12179.nr 0.301
(1.70)
12182.nr 0.515**
(2.93)
12220.nr 0.673***
(3.81)
12221.nr -0.121
(-0.66)
12245.nr -0.110
(-0.63)
12276.nr 0.655***
(3.69)
12385.nr 0.819***
(4.57)
12410.nr 0.0399
(0.22)
12420.nr 0.840***
(4.74)
12433.nr 0.393*
(2.23)
12451.nr 0.431*
(2.45)
12477.nr 1.004***
(5.62)
12500.nr 0.222
(1.25)
12534.nr 0.942***
(5.35)
12548.nr 0.347
(1.93)
_cons -0.445*** 1.426*** 0.933***
(-14.96) (77.75) (7.44)
-------------------------------------------------
N 4360 4360 4360
-------------------------------------------------
t statistics in parentheses
* p<0.05, ** p<0.01, *** p<0.001Practical Tips
Notice that the parameter \(\delta\) does not have meaning.
\[y_{i,t} = \alpha + \beta_1 x_{i,t} + \delta FE + \epsilon_{i,t}\]
In fact, the previous slides have shown that you will find the same results of a FE model if you include the dummies for the units in the panel (i.e., dummies for the firms or individuals, etc.).
This is called least squares dummy variable (LSDV) model.
the SE are also identical to the within-transformation model.
But the R2 of the LSDV will be very high because you are including a lot of “explanatory variables”.
Note
At the end of the day, you will use the package for the unit’s FE (i.e., the firm), and will include the additional FE as dummies, just like a LSDV model.
Practical Tips
When you estimate a LSDV, the software will inform an \(\alpha\).
But this coefficient has no interpretation whatsoever.
- it will be FE for the dropped unit of FE.
You can simply ignore it, you even don’t need to include in your final table.
No problem if you do, just don’t make inferences from it.
Practical Tips
A FE model helps a lot, but it only does what it can do.
That is, FE models do not capture time-variant unobserved heterogeneity.
Also, if you have constant Xs in your model, you will have to drop them.
More technically, if there is no within-variation in a X, you cannot include it (the software will drop them).
For instance, the software will drop \(year_{birth}\) below if you include CEO FE.
\[Y_{i,t} = \alpha + \beta_1 year_{birth} + CEO \;FE + ... + \epsilon_{i,t}\]
If you attempt to include the CEO FE manually, the software will drop a random CEO FE or the variable \(year_{birth}\). If you get a beta for \(year_{birth}\) it has no meaning.
Practical Tips
Adding many FE can demand a lot of computational power.
Consider the multidimensional model as follows:
\[Y_{i,t} = \alpha + \beta_1 X_{i,t} + Firm \;FE + Year\; FE + Year.Industry \;FE + CEO \;FE + ... + \epsilon_{i,t}\]
It would take a while to estimate in an average computer.
Random Effects
Random Effects
Remember that:
\[\epsilon_{i,t} = c_i + \mu_{i,t}\]
The most important thing here is whether \(x_{it}\) and \(c_i\) are correlated.
If they are, you should estimate Fixed Effects
If \(x_{it}\) and \(c_i\) are not correlated, then \(c_i\) is referred to as a random effect.
- Endogeneity is not a concern; however, the computation of standard errors is affected.
But, if the \(x_{it}\) and \(c_i\) are not correlated, there is no endogeneity concern.
\(c_i\) can be let as part of the \(\epsilon_{i,t}\) without bias in the estimated betas.
Random Effects
Additionally, the assumption that \(x_{it}\) and \(c_i\) are not correlated is rather strong and not practical to most applications of corporate finance, economics or public policy.
RE is a model not used often. Cunningham does not even discuss it.
If the key explanatory variable is constant over time, we cannot use FE to estimate its effect on y.
Of course, we can only use RE because we are willing to assume the unobserved effect is uncorrelated with all explanatory variables.
Typically, if one uses RE, and as many time-constant controls as possible are included among the explanatory variables (with an FE analysis, it is not necessary to include such controls) RE is preferred to pooled OLS because RE is generally more efficient.
(Wooldridge, p.496)
Random Effects
R
# Load necessary packages
library(plm)
library(jtools)
library(foreign)
data <- read.dta("files/WAGEPAN.dta")
pdata <- pdata.frame(data, index = c("nr", "year"))
po_model <- lm(lwage ~ expersq + married + union + factor(year) + educ + black + hisp + exper, data = data)
fe_model <- plm(lwage ~ expersq + married + union + factor(year) + educ + black + hisp + exper, data = pdata, model = "within")
re_model <- plm(lwage ~ expersq + married + union + factor(year) + educ + black + hisp + exper, data = pdata, model = "random")
stargazer(po_model, fe_model , re_model ,title = "Regression Results", column.labels=c("OLS","FE","RE"), type = "text")
Regression Results
==================================================================================
Dependent variable:
--------------------------------------------------------------
lwage
OLS panel
linear
OLS FE RE
(1) (2) (3)
----------------------------------------------------------------------------------
expersq -0.002*** -0.005*** -0.005***
(0.001) (0.001) (0.001)
married 0.108*** 0.047** 0.064***
(0.016) (0.018) (0.017)
union 0.182*** 0.080*** 0.106***
(0.017) (0.019) (0.018)
factor(year)1981 0.058* 0.151*** 0.040
(0.030) (0.022) (0.025)
factor(year)1982 0.063* 0.253*** 0.031
(0.033) (0.024) (0.032)
factor(year)1983 0.062* 0.354*** 0.020
(0.037) (0.029) (0.042)
factor(year)1984 0.090** 0.490*** 0.043
(0.040) (0.036) (0.051)
factor(year)1985 0.109** 0.617*** 0.058
(0.043) (0.045) (0.061)
factor(year)1986 0.142*** 0.765*** 0.092
(0.046) (0.056) (0.071)
factor(year)1987 0.174*** 0.925*** 0.135*
(0.049) (0.069) (0.081)
educ 0.091*** 0.092***
(0.005) (0.011)
black -0.139*** -0.139***
(0.024) (0.048)
hisp 0.016 0.022
(0.021) (0.043)
exper 0.067*** 0.106***
(0.014) (0.015)
Constant 0.092 0.024
(0.078) (0.151)
----------------------------------------------------------------------------------
Observations 4,360 4,360 4,360
R2 0.189 0.181 0.181
Adjusted R2 0.187 0.061 0.178
Residual Std. Error 0.480 (df = 4345)
F Statistic 72.459*** (df = 14; 4345) 83.851*** (df = 10; 3805) 957.774***
==================================================================================
Note: *p<0.1; **p<0.05; ***p<0.01Stata
use "files/WAGEPAN.dta" , clear
xtset nr year
eststo: qui reg lwage expersq married union i.year educ black hisp exper
eststo: qui xtreg lwage expersq married union i.year educ black hisp exper , fe
eststo: qui xtreg lwage expersq married union i.year educ black hisp exper , re
esttab , mtitles("OLS" "FE" "RE") compressPanel variable: nr (strongly balanced)
Time variable: year, 1980 to 1987
Delta: 1 unit
(est1 stored)
(est2 stored)
(est3 stored)
-------------------------------------------------
(1) (2) (3)
OLS FE RE
-------------------------------------------------
expersq -0.00241** -0.00519*** -0.00472***
(-2.94) (-7.36) (-6.85)
married 0.108*** 0.0467* 0.0640***
(6.90) (2.55) (3.81)
union 0.182*** 0.0800*** 0.106***
(10.63) (4.14) (5.94)
1980.year 0 0 0
(.) (.) (.)
1981.year 0.0583 0.151*** 0.0405
(1.92) (6.89) (1.64)
1982.year 0.0628 0.253*** 0.0309
(1.89) (10.36) (0.96)
1983.year 0.0620 0.354*** 0.0203
(1.69) (12.12) (0.49)
1984.year 0.0905* 0.490*** 0.0431
(2.26) (13.53) (0.84)
1985.year 0.109* 0.617*** 0.0578
(2.52) (13.65) (0.94)
1986.year 0.142** 0.765*** 0.0919
(3.06) (13.64) (1.29)
1987.year 0.174*** 0.925*** 0.135
(3.52) (13.45) (1.66)
educ 0.0913*** 0 0.0919***
(17.44) (.) (8.62)
black -0.139*** 0 -0.139**
(-5.90) (.) (-2.92)
hisp 0.0160 0 0.0217
(0.77) (.) (0.51)
exper 0.0672*** 0 0.106***
(4.91) (.) (6.88)
_cons 0.0921 1.426*** 0.0236
(1.18) (77.75) (0.16)
-------------------------------------------------
N 4360 4360 4360
-------------------------------------------------
t statistics in parentheses
* p<0.05, ** p<0.01, *** p<0.001FE vs. RE
FE vs. RE
The idea is that one uses the random effects estimates unless the Hausman test rejects.
In practice, a failure to reject means either that the RE and FE estimates are sufficiently close so that it does not matter which is used, or the sampling variation is so large in the FE estimates that one cannot conclude practically significant differences are statistically significant. (Wooldridge)
If the p-value of the Hausman test is significant then use FE, if not use RE.
FE vs. RE
Stata
Panel variable: nr (strongly balanced)
Time variable: year, 1980 to 1987
Delta: 1 unit
---- Coefficients ----
| (b) (B) (b-B) sqrt(diag(V_b-V_B))
| fe_model re_model Difference Std. err.
-------------+----------------------------------------------------------------
expersq | -.0051855 -.0047239 -.0004616 .0001443
married | .0466804 .063986 -.0173057 .0073414
union | .0800019 .1061344 -.0261326 .0073572
year |
1981 | .1511912 .040462 .1107292 .
1982 | .2529709 .0309212 .2220497 .
1983 | .3544437 .0202806 .3341631 .
1984 | .4901148 .0431187 .4469961 .
1985 | .6174822 .0578154 .5596668 .
1986 | .7654965 .0919475 .673549 .
1987 | .9250249 .1349289 .790096 .
------------------------------------------------------------------------------
b = Consistent under H0 and Ha; obtained from xtreg.
B = Inconsistent under Ha, efficient under H0; obtained from xtreg.
Test of H0: Difference in coefficients not systematic
chi2(10) = (b-B)'[(V_b-V_B)^(-1)](b-B)
= 26.36
Prob > chi2 = 0.0033
(V_b-V_B is not positive definite)First differences
First differences
In most applications, the main reason for collecting panel data is to allow for the unobserved effect, \(c_i\), to be correlated with the explanatory variables.
For example, in the crime equation, we want to allow the unmeasured city factors in \(c_i\) that affect the crime rate also to be correlated with the unemployment rate.
It turns out that this is simple to allow: because \(c_i\) is constant over time, we can difference the data across the two years.
More precisely, for a cross-sectional observation \(i\), write the two years as:
\[y_{i,1} = \beta_0 + \beta_1 x_{i,1} + c_i + \mu_{i,1}, t=1\]
\[y_{i,2} = (\beta_0 + \delta_0) + \beta_1 x_{i,2} + c_i + \mu_{i,2}, t=2\]
If we subtract the second equation from the first, we obtain
\[(y_{i,2} - y_{i,1}) = \delta_0 + \beta_1 (x_{i,2} - x_{i,1}) + (\mu_{i,2}-\mu_{i,1})\]
\[\Delta y_{i} = \delta_0 + \beta_1 \Delta x_{i} + \Delta \mu_{i}\]
First differences
So, rather than subtracting the group mean of each variable, you subtract the lagged observation.
Not hard to see that, when t=2, FE and FD will give identical solutions
FE is more efficient if disturbances \(\mu_{i,t}\) have low serial correlation
FD is more efficient if disturbance \(\mu_{i,t}\) follow a random walk
At the end of the day, you can estimate both.
Empirical research usually estimate FD only in specific circumstances, when they are interested in how changes of X affect changes of Y.
Things like stationarity or trends are often not concerns in panel data
- where N is 10 to 20
First differences
R
# Load necessary packages
# Load necessary libraries
library(plm)
library(lmtest)
library(stargazer)
data <- read.dta("files/WAGEPAN.dta")
pdata <- pdata.frame(data, index = c("nr", "year"))
ols_model <- lm(lwage ~ expersq + married + union + factor(year) + educ + black + hisp + exper, data = pdata)
fe_model <- plm(lwage ~ expersq + married + union + educ + black + hisp + exper, data = pdata, model = "within")
re_model <- plm(lwage ~ expersq + married + union + educ + black + hisp + exper, data = pdata, model = "random")
fd_model <- plm(lwage ~ expersq + married + union + educ + black + hisp + exper, data = pdata, model = "fd")
stargazer(ols_model, fe_model ,re_model, fd_model,title = "Regression Results", type = "text")
Regression Results
==========================================================================================================
Dependent variable:
--------------------------------------------------------------------------------------
lwage
OLS panel
linear
(1) (2) (3) (4)
----------------------------------------------------------------------------------------------------------
expersq -0.002*** -0.004*** -0.004*** -0.004***
(0.001) (0.001) (0.001) (0.001)
married 0.108*** 0.045** 0.063*** 0.038*
(0.016) (0.018) (0.017) (0.023)
union 0.182*** 0.082*** 0.107*** 0.043**
(0.017) (0.019) (0.018) (0.020)
factor(year)1981 0.058*
(0.030)
factor(year)1982 0.063*
(0.033)
factor(year)1983 0.062*
(0.037)
factor(year)1984 0.090**
(0.040)
factor(year)1985 0.109**
(0.043)
factor(year)1986 0.142***
(0.046)
factor(year)1987 0.174***
(0.049)
educ 0.091*** 0.101***
(0.005) (0.009)
black -0.139*** -0.144***
(0.024) (0.048)
hisp 0.016 0.020
(0.021) (0.043)
exper 0.067*** 0.117*** 0.112***
(0.014) (0.008) (0.008)
Constant 0.092 -0.107 0.116***
(0.078) (0.111) (0.020)
----------------------------------------------------------------------------------------------------------
Observations 4,360 4,360 4,360 3,815
R2 0.189 0.178 0.178 0.004
Adjusted R2 0.187 0.060 0.177 0.003
Residual Std. Error 0.480 (df = 4345)
F Statistic 72.459*** (df = 14; 4345) 206.375*** (df = 4; 3811) 943.951*** 5.362*** (df = 3; 3811)
==========================================================================================================
Note: *p<0.1; **p<0.05; ***p<0.01Stata
use "files/WAGEPAN.dta" , clear
xtset nr year
eststo: qui reg lwage expersq married union i.year educ black hisp exper
eststo: qui xtreg lwage expersq married union i.year educ black hisp exper , fe
eststo: qui xtreg lwage expersq married union i.year educ black hisp exper , re
eststo: qui reg D.lwage D.expersq D.married D.union i.year D.educ D.black D.hisp D.exper
esttab , mtitles("OLS" "FE" "RE" "FD") compressPanel variable: nr (strongly balanced)
Time variable: year, 1980 to 1987
Delta: 1 unit
(est1 stored)
(est2 stored)
(est3 stored)
(est4 stored)
--------------------------------------------------------------
(1) (2) (3) (4)
OLS FE RE FD
--------------------------------------------------------------
expersq -0.00241** -0.00519*** -0.00472***
(-2.94) (-7.36) (-6.85)
married 0.108*** 0.0467* 0.0640***
(6.90) (2.55) (3.81)
union 0.182*** 0.0800*** 0.106***
(10.63) (4.14) (5.94)
1980.year 0 0 0
(.) (.) (.)
1981.year 0.0583 0.151*** 0.0405 0
(1.92) (6.89) (1.64) (.)
1982.year 0.0628 0.253*** 0.0309 -0.0482
(1.89) (10.36) (0.96) (-1.77)
1983.year 0.0620 0.354*** 0.0203 -0.0479
(1.69) (12.12) (0.49) (-1.70)
1984.year 0.0905* 0.490*** 0.0431 -0.0122
(2.26) (13.53) (0.84) (-0.41)
1985.year 0.109* 0.617*** 0.0578 -0.0208
(2.52) (13.65) (0.94) (-0.65)
1986.year 0.142** 0.765*** 0.0919 0.00151
(3.06) (13.64) (1.29) (0.04)
1987.year 0.174*** 0.925*** 0.135 0.0167
(3.52) (13.45) (1.66) (0.45)
educ 0.0913*** 0 0.0919***
(17.44) (.) (8.62)
black -0.139*** 0 -0.139**
(-5.90) (.) (-2.92)
hisp 0.0160 0 0.0217
(0.77) (.) (0.51)
exper 0.0672*** 0 0.106***
(4.91) (.) (6.88)
D.expersq -0.00575**
(-2.65)
D.married 0.0381
(1.66)
D.union 0.0411*
(2.09)
oD.educ 0
(.)
oD.black 0
(.)
oD.hisp 0
(.)
oD.exper 0
(.)
_cons 0.0921 1.426*** 0.0236 0.156***
(1.18) (77.75) (0.16) (6.36)
--------------------------------------------------------------
N 4360 4360 4360 3815
--------------------------------------------------------------
t statistics in parentheses
* p<0.05, ** p<0.01, *** p<0.001Lagged independent variables
Lagged independent variables
When you have a panel data and are concerned with simultaneity between Y and X, you can endeavor in lagging the Xs.
\[y_{i,t} = \beta_0 + \beta_1 x_{i,t-1} + c_i + \mu_{i,t}\]
As a matter of fact, this is often expected in finance research.
There is a limitation, however.
The usual proxy of corporate finance research is highly autocorrelated.
- e.g., total assets do not vary much throughout time.
Thus, lagging the X often does not make much of a difference.
Tip
Always do it. Otherwise, you will have to explain why you didn’t do it.
Lagged dependent variables
Lagged dependent variables
Sometimes you may have something like
\[y_{i,t} = \beta_0 + \beta_1 y_{i,t-1}+ \beta_2 x_{i,t} + c_i + \mu_{i,t}\]
This is called a Dynamic Panel Model. It includes \(y_{i,t-1}\) as X.
Consider a FE model.
\[y_{i,t} - \bar{y_i} = \beta_0 + \gamma_1 (y_{i,t-1} - \bar{y}_{i,t-1}) + \omega_2 (x_{i,t-1} - \bar{x_i} ) + (FE_i - \bar{FE}_i) + (\mu_{i,t} - \bar{\mu}_i )\]
The within transformation removes the time-invariant unobserved heterogeneity from the model.
However, it introduces a correlation between the transformed lag \((y_{i,t−1}−\bar{y}_{i,t-1})\) and the transformed error \((\mu_{i,t−1}−\bar{\mu}_{i,t-1})\) because the average error (\(\bar{\mu} = \sum_{i=1}^{T} \mu_{i,t}\)) includes \(\mu_{i,t-1}\), which is also “included” in \(y_{i,t−1}\)
- \(y_{i,t-1} = \beta_0 + \beta_1 y_{i,t-2}+ \beta_2 x_{i,t-1} + c_i + \mu_{i,t-1}\)
Lagged dependent variables
The bias declines with panel length because \(\epsilon_{i,t−1}\) becomes a smaller component of the average error term as T increases.
In other words, with higher T the correlation between the lagged dependent variable and the regression errors becomes smaller.
Flannery and Hankins (2013) have a good review with applications in corporate finance.
They conclude that FE is biased when estimating these models.
They suggest to estimate Sys-GMM or Least Squares Dummy Variable Correction. We do not discuss these models in the course.
Selection Bias
Selection Bias
Back to the selection bias example of before.
Imagine that John and Mary are moving to the north of Canada.
John has a history of respiratory disease and decide to buy insurance.
Mary does not have a history of respiratory disease and decide not to buy insurance.
| Default | John | Mary |
|---|---|---|
| State of insurance | 1 | 0 |
| Situation without insurance | 3 |
5 |
| Situation with insurance | 4 | 5 |
| Observed | 4 | 5 |
| Effect | ? | ? |
\[(Y_{1,john} - Y_{0,john}) + (Y_{1,Mary}- Y_{0,Mary}) = 4 - 3 + 5 - 5 = 0.5\]
Selection Bias
Rearranging the terms:
\[(Y_{1,john} - Y_{0,Mary}) + (Y_{1,Mary} - Y_{0,john}) = (4 - 5) + (5 - 3) = 0.5\] \[We\;see + We\;do\;not\;see = (4 - 5) + (5 - 3) = 0.5\]
The term \((Y_{1,Mary} - Y_{0,john}) = (5 - 3) = 2\) is the selection bias.
It exists because we are comparing two people that should not be compared.
Selection Bias
Some notation:
\(d=1\) for the treated units (treatment group)
\(d=0\) for the treated units (control group)
\(Y_{i}\) = Potential outcome of individual i.
\(Y_{i,1}\) or \(Y(1)\) = Potential outcome of individual i, treatement group.
\(Y_{i,0}\) or \(Y(0)\) = Potential outcome of individual i, control group.
Selection Bias
Some notation:
These are the representations of the causal effect we often want to estimate.
Average Treatment Effect:
ATE = \(\frac{1}{N} (E[Y_{i,1}] - E[Y_{i,0}])\)
Average Treatment Effect on the treated:
ATET = \(\frac{1}{N} (E[Y_{i,1}|D_i=1] - E[Y_{i,0}|D_i=1])\)
Average Treatment Effect on the untreated:
ATEU = \(\frac{1}{N} (E[Y_{i,1}|D_i=0] - E[Y_{i,0}|D_i=0])\)
Of course, again, we cannot observe both potential outcomes of the same unit i.
Selection Bias
When dealing with causal inference, we have to find ways to approximate what the hidden potential outcome of the treated units is.
That is, the challenge in identifying causal effects is that the untreated potential outcomes, \(Y_{i,0}\), are never observed for the treated group (\(D_i= 1\)). The “second” term in the following equation:
ATET = \(\frac{1}{N} (E[Y_{i,1}|D_i=1] - E[Y_{i,0}|D_i=1])\)
We need an empirical design to “observe” what we do not really observe (i.e., the counterfactual).
Selection Bias
Many options:
- Matching/Balancing
- Difference-in-differences (DiD)
- Instrumental variables
- Regression discontinuity design (RDD)
- Synthetic control (Synth)
Selection Bias
The process of finding units that are comparable is called matching.
Before we continue…
We will match on observables. We cannot be on unobservables.
Thus, you may want to write in your article “selection bias due to observables”.
Cunningham:
Propensity score matching has not seen as wide adoption among economists as in other nonexperimental methods like regression discontinuity or difference-in-differences. The most common reason given for this is that economists are oftentimes skeptical that CIA can be achieved in any dataset almost as an article of faith. This is because for many applications, economists as a group are usually more concerned about selection on unobservables than they are selection on observables, and as such, they reach for matching methods less often.
CIA = CMI
Matching
Matching
Matching aims to compare the outcomes between observations that have the same values of all control variables, except that one unit is treated and the other is not.
In this literature, the control variables used to matched are often called covariates.
That is, for each treated unit, the researcher finds an untreated unit that is similar in all covariates.
The implication is that the researcher can argue that “units are comparable after matching”.
Matching
The easiest to see is exact matching: it matches observations that have the exact same values.
It might be doable if you have only one covariate.
Naturally, if you have only one covariate, you might still be left with some selection bias.
In the previous example, health history is one important covariate that makes John and Mary different.
But what about life style? Nutrition? Etc.
As the number of covariates grow, you cannot pursue exact matching. That is the job of PSM.
Matching
In exact matching, the causal effect estimator (ATET) is:
\[ATET = \frac{1}{N} \sum (E[Y_{i}] - E[Y_{j(i)}] | D_i=1)\]
Where \(Y_{j(i)}\) is the j-th unit matched to the i-th unit based on the j-th being “closest to” the i-th unit for some covariate.
For instance, let’s say that a unit in the treatment group has a covariate with a value of 2 and we find another unit in the control group (exactly one unit) with a covariate value of 2.
Then we will impute the treatment unit’s missing counterfactual with the matched unit’s, and take a difference.
Matching
Consider the following dataset from Cunningham:
Matching
Average ages are very different. The salary of a 24 yrs old person is quite different than the salary of a 32 yrs person.
R
# Load necessary packages
library(tidyverse)
library(haven)
library(knitr)
library(kableExtra)
read_data <- function(df)
{
full_path <- paste("https://github.com/scunning1975/mixtape/raw/master/",df, sep = "")
df <- read_dta(full_path)
return(df)
}
training_example <- read_data("training_example.dta") %>% slice(1:20)
summary(training_example$age_treat) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
18.00 20.25 23.00 24.30 28.50 33.00 10 Min. 1st Qu. Median Mean 3rd Qu. Max.
18.00 23.50 31.50 31.95 39.00 51.00 R
# Load necessary packages
library(tidyverse)
library(haven)
library(knitr)
library(kableExtra)
read_data <- function(df)
{
full_path <- paste("https://github.com/scunning1975/mixtape/raw/master/",df, sep = "")
df <- read_dta(full_path)
return(df)
}
training_example <- read_data("training_example.dta") %>% slice(1:20)
ggplot(training_example, aes(x=age_treat)) +
stat_bin(bins = 10, na.rm = TRUE)
R
# Load necessary packages
library(tidyverse)
library(haven)
library(knitr)
library(kableExtra)
read_data <- function(df)
{
full_path <- paste("https://github.com/scunning1975/mixtape/raw/master/",df, sep = "")
df <- read_dta(full_path)
return(df)
}
training_example <- read_data("training_example.dta") %>% slice(1:20)
ggplot(training_example, aes(x=age_control)) +
stat_bin(bins = 10, na.rm = TRUE)
R
# Load necessary packages
library(tidyverse)
library(haven)
library(knitr)
library(kableExtra)
read_data <- function(df)
{
full_path <- paste("https://github.com/scunning1975/mixtape/raw/master/",df, sep = "")
df <- read_dta(full_path)
return(df)
}
training_example <- read_data("training_example.dta") %>% slice(1:20)
ggplot(training_example, aes(x=age_matched)) +
stat_bin(bins = 10, na.rm = TRUE)
Matching
In this example, you are literally finding the units in the control group that have the same age as the units in the treatment group.
You are exact matching 1-by-1 in this example.
You have only one covariate, i.e., age.
Distance Matching
Distance Matching
The last example was simple because you could exact match.
If you cannot find one exact match, you need an approximate match.
In order to do that, you have to use distance matching.
Distance matching minimizes the distance (i.e., how far the covariates are from each other) between the treatment and control groups.
Distance Matching
Euclidean distance = \(|X_i-X_j|=\sqrt{(X_i-X_j)'(X_i-X_j)}=\sqrt{\sum_{n=1}^k(X_{n,i}-X_{n,j})^2}\)
Distance Matching
Normalized Euclidean distance = \(|X_i-X_j|=\sqrt{(X_i-X_j)'\hat{V}^{-1}(X_i-X_j)}=\sqrt{\sum_{n=1}^k\frac{(X_{n,i}-X_{n,j})}{\sigma^2_n}}\)
The problem with this measure of distance is that the distance measure itself depends on the scale of the variables themselves.
For this reason, researchers typically will use some modification of the Euclidean distance, such as the normalized Euclidean distance, or they’ll use a wholly different alternative distance.
The normalized Euclidean distance is a commonly used distance, and what makes it different is that the distance of each variable is scaled by the variable’s variance.
Distance Matching
Mahalanobis distance = \(|X_i-X_j|=\sqrt{(X_i-X_j)'\hat{\sum_x}^{-1}(X_i-X_j)}\)
Where \(\hat{\sum_x}\) is the sample covariance matrix of X.
Distance Matching
Distance matching only goes so far…
… the larger the dimensionality, the harder is to use distance matching.
As sample size increases, for a given N of covariates, the matching discrepancies tend to zero.
But, the more covariates, the longer it takes.
At the end of the day, it is preferable to have many covariates, but it is makes distance matching harder.
Coarsened Exact Matching (CER)
Coarsened Exact Matching (CER)
In coarsened exact matching, something only counts as a match if it exactly matches on each matching variable.
The “coarsened” part comes in because, if you have any continuous variables to match on, you need to “coarsen” them first by putting them into bins, rather than matching on exact values.
Coarsening means creating bins. Fewer bins makes exact matches more likely.
CER is not used much in empirical research in finance. It is used more in the big data realm when you have many variables to match.
Propensity-score matching (PSM)
Propensity-score matching (PSM)
PSM is one way to matching using many covariates.
PSM aggregates all covariates into one score (propensity-score), which is the likelihood of receiving the treatment.
The idea is to match units that, based on observables, have the same probability (called propensity-score) of being treated.
The idea is to estimate a probit (default in stata) or logit model (fist stage):
\[P(D=1|X)\]
The propensity-score is the predicted probability of a unit being treated given all covariates X. The p-score is just a single number.
Propensity-score matching (PSM)
Considerations in PSM.
- How many neighbors to match?
- Nearest neighbor, radius or kernel?
With or without replacement?
With or without common support?
- Common support: imposes a common support by dropping treatment observations whose pscore is higher than the maximum or less than the minimum pscore of the controls.
- It is expected that, after PSM, you show the overlap of propensity-scores.
Propensity-score matching (PSM)
The y-axis is the propensity-score.
Propensity-score matching (PSM)
Nearest matching: Find the observation closest to (\(min|p_i-p_j|\))
Propensity-score matching (PSM)
Kernel matching: Each treated observation i is matched with several control observations, with weights inversely proportional to the distance between treated and control observations.
Propensity-score matching (PSM)
Radius matching: Each treated observation i is matched with control observations j that fall within a specified radius.
\[|p_i-p_j| <r\]
Propensity-score matching (PSM)
Common support: Restrict matching only based on the common range of propensity scores.
Propensity-score matching (PSM)
Seems good overlap, but “good” is arbitrary.
Propensity-score matching (PSM)
Seems bad overlap
Propensity-score matching (PSM)
Seems good overlap, but “good” is arbitrary.
Propensity-score matching (PSM)
Seems bad overlap
Propensity-score matching (PSM)
Propensity-score matching (PSM)
Propensity-score matching (PSM)
Example
Example
Let’s practice with an example. 185 treated units vs 15,992 control units.
R
# Load necessary packages
# Load necessary libraries
library(haven)
library(psych)
data <- read_dta("files/cps1re74.dta")
summary_stats <- by(data, data$treat, FUN = function(group) {
c(
mean = mean(group$age, na.rm = TRUE),
variance = var(group$age, na.rm = TRUE),
skewness = skew(group$age, na.rm = TRUE),
count = length(group$age)
)
})
summary_df <- as.data.frame(do.call(rbind, summary_stats))
colnames(summary_df) <- c("mean", "variance", "skewness", "count")
print(summary_df) mean variance skewness count
0 33.22524 121.9968 0.3477684 15992
1 25.81622 51.1943 1.1063375 185Python
import pandas as pd
from scipy.stats import skew
import statsmodels.api as sm
data = pd.read_stata("files/cps1re74.dta")
grouped_data = data.groupby('treat')['age'].agg(['mean', 'var', lambda x: skew(x, nan_policy='omit'), 'count']).reset_index()
grouped_data.columns = ['treat', 'mean', 'variance', 'skewness', 'count']
print(grouped_data) treat mean variance skewness count
0 0 33.225238 121.996792 0.347801 15992
1 1 25.816216 51.194301 1.115369 185Stata
(DW Subset of LaLonde Data)
------------------------------------------------------------
mean variance skewness count
------------------------------------------------------------
0
age 33.225 121.997 0.348 15992
black 0.074 0.068 3.268 15992
educ 12.028 8.242 -0.423 15992
------------------------------------------------------------
1
age 25.816 51.194 1.115 185
black 0.843 0.133 -1.888 185
educ 10.346 4.043 -0.721 185
------------------------------------------------------------Example
Clearly, the treated group is younger, mainly black, and less educated.
Also note that the variance and skewness of the two subsamples are different.
If we were to use these two subsamples in any econometric analysis without preprocessing to make them comparable, we would likely have coefficients biased by selection bias.
Therefore, it is important to perform some matching method.
Let’s start with Propensity Score Matching (PSM). We will use the simplest matching, that is, without using any additional functions.
Example
Nearest with noreplacement.
R
Call:
matchit(formula = treat ~ age + black + educ, data = data, method = "nearest")
Summary of Balance for All Data:
Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean
distance 0.1445 0.0099 1.3615 7.5662 0.4987
age 25.8162 33.2252 -1.0355 0.4196 0.1863
black 0.8432 0.0735 2.1171 . 0.7697
educ 10.3459 12.0275 -0.8363 0.4905 0.0908
eCDF Max
distance 0.7741
age 0.3427
black 0.7697
educ 0.4123
Summary of Balance for Matched Data:
Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean
distance 0.1445 0.1443 0.0020 1.0039 0.0002
age 25.8162 25.7081 0.0151 0.9244 0.0073
black 0.8432 0.8432 0.0000 . 0.0000
educ 10.3459 10.4054 -0.0296 0.7190 0.0117
eCDF Max Std. Pair Dist.
distance 0.0162 0.0029
age 0.0270 0.1481
black 0.0000 0.0000
educ 0.0432 0.2554
Sample Sizes:
Control Treated
All 15992 185
Matched 185 185
Unmatched 15807 0
Discarded 0 0Stata
(DW Subset of LaLonde Data)
Probit regression Number of obs = 16,177
LR chi2(3) = 752.47
Prob > chi2 = 0.0000
Log likelihood = -634.83401 Pseudo R2 = 0.3721
------------------------------------------------------------------------------
treat | Coefficient Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
age | -.0379829 .0042976 -8.84 0.000 -.046406 -.0295598
black | 1.700675 .0793898 21.42 0.000 1.545074 1.856277
educ | -.0806962 .0142167 -5.68 0.000 -.1085604 -.052832
_cons | -.9031083 .2123282 -4.25 0.000 -1.319264 -.4869526
------------------------------------------------------------------------------
psmatch2: weight of matched controls
-------------------------------------------------------------
Percentiles Smallest
1% 1 1
5% 1 1
10% 1 1 Obs 370
25% 1 1 Sum of wgt. 370
50% 1 Mean 1
Largest Std. dev. 0
75% 1 1
90% 1 1 Variance 0
95% 1 1 Skewness .
99% 1 1 Kurtosis .Example
Notice that we are creating weights now
(DW Subset of LaLonde Data)
psmatch2: weight of matched controls
-------------------------------------------------------------
Percentiles Smallest
1% .0024355 .0007862
5% .0024375 .0024348
10% .00244 .0024348 Obs 16,177
25% .0024517 .0024348 Sum of wgt. 16,177
50% .0024919 Mean .022872
Largest Std. dev. .1130791
75% .0026476 1
90% .0038379 1 Variance .0127869
95% .0876547 1 Skewness 7.604874
99% 1 1 Kurtosis 64.26276Example
Now, the descriptive statistics are much closer
R
library(haven)
library(MatchIt)
#install.packages("e1071")
library(e1071)
data <- read_dta("files/cps1re74.dta")
model <- matchit(treat ~ age + black + educ, data = data, method = "exact")
matched_data <- match.data(model)
summary_stats <- by(matched_data, matched_data$treat, function(x) {
c(mean(x$age), var(x$age), skewness(x$age), length(x$age))
})
result_df <- data.frame(
Treatment = c("Control", "Treated"),
Mean_Age = sapply(summary_stats, function(x) x[1]),
Variance_Age = sapply(summary_stats, function(x) x[2]),
Skewness_Age = sapply(summary_stats, function(x) x[3]),
Count = sapply(summary_stats, function(x) x[4])
)
print(result_df) Treatment Mean_Age Variance_Age Skewness_Age Count
0 Control 25.58786 39.16294 0.7826941 2191
1 Treated 25.51807 51.59664 1.1298334 166Stata
(DW Subset of LaLonde Data)
------------------------------------------------------------
mean variance skewness count
------------------------------------------------------------
0
age 27.033 85.548 1.077 15992
black 0.791 0.165 -1.434 15992
educ 10.710 8.146 -0.883 15992
------------------------------------------------------------
1
age 25.816 51.194 1.115 185
black 0.843 0.133 -1.888 185
educ 10.346 4.043 -0.721 185
------------------------------------------------------------Entropy Balancing
Entropy Balancing
Here, instead of matching units, we reweight the observations such that the moments of the distributions (mean, variance, skewness) are similar.
The ebalance function implements a reweighting scheme. The user starts by choosing the covariates that should be included in the reweighting.
For each covariate, the user then specifies a set of balance constraints (in Equation 5) to equate the moments of the covariate distribution between the treatment and the reweighted control group.
The moment constraints may include the mean (first moment), the variance (second moment), and the skewness (third moment).
The outcome is a vector containing the weights to weight the observations, such that the weighted average, weighted variance, and weighted skewness of the covariates in control group are similar to those in the treatment group
Entropy Balancing
R
Converged within tolerance [1] 25.8162162 10.3459459 0.8432432[1] 25.8163688 10.3460391 0.8431526[1] 33.22523762 12.02751376 0.07353677(DW Subset of LaLonde Data)
Data Setup
Treatment variable: treat
Covariate adjustment: age black educ (1st order). age black educ (2nd order). a
> ge black educ (3rd order).
Optimizing...
Iteration 1: Max Difference = 580799.347
Iteration 2: Max Difference = 213665.688
Iteration 3: Max Difference = 78604.7628
Iteration 4: Max Difference = 28918.6249
Iteration 5: Max Difference = 10640.1108
Iteration 6: Max Difference = 3915.82197
Iteration 7: Max Difference = 1442.09731
Iteration 8: Max Difference = 532.07826
Iteration 9: Max Difference = 197.376777
Iteration 10: Max Difference = 74.6380533
Iteration 11: Max Difference = 29.9524313
Iteration 12: Max Difference = 11.4337344
Iteration 13: Max Difference = 4.43722698
Iteration 14: Max Difference = 1.76899046
Iteration 15: Max Difference = .420548538
Iteration 16: Max Difference = .037814194
Iteration 17: Max Difference = .001164231
maximum difference smaller than the tolerance level; convergence achieved
Treated units: 185 total of weights: 185
Control units: 15992 total of weights: 185
Before: without weighting
| Treat | Control
| mean variance skewness | mean variance
-------------+---------------------------------+----------------------
age | 25.82 51.19 1.115 | 33.23 122
black | .8432 .1329 -1.888 | .07354 .06813
educ | 10.35 4.043 -.7212 | 12.03 8.242
| Control
| skewness
-------------+-----------
age | .3478
black | 3.268
educ | -.4233
After: _webal as the weighting variable
| Treat | Control
| mean variance skewness | mean variance
-------------+---------------------------------+----------------------
age | 25.82 51.19 1.115 | 25.8 51.17
black | .8432 .1329 -1.888 | .8421 .133
educ | 10.35 4.043 -.7212 | 10.34 4.04
| Control
| skewness
-------------+-----------
age | 1.122
black | -1.877
educ | -.7121 Entropy Balancing
Stata
(DW Subset of LaLonde Data)
------------------------------------------------------------
mean variance skewness count
------------------------------------------------------------
0
age 25.801 51.167 1.122 15992
black 0.842 0.133 -1.877 15992
educ 10.340 4.040 -0.712 15992
------------------------------------------------------------
1
age 25.816 51.194 1.115 185
black 0.843 0.133 -1.888 185
educ 10.346 4.043 -0.721 185
------------------------------------------------------------THANK YOU!
